- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Distribution Modulo One and Diophantine Approximation

Publisher:
Cambridge University Press
Publication Date:
2012
Number of Pages:
300
Format:
Hardcover
Series:
Cambridge Tracts in Mathematics 193
Price:
80.00
ISBN:
9780521111690
Category:
Monograph
[Reviewed by , on ]
Underwood Dudley
11/1/2012
A sequence of real numbers is uniformly distributed (mod 1) if its fractional parts distribute themselves along the unit interval as if they were random. That is, in the limit, the proportion of them in an interval of length d is d.
In 1916 Hermann Weyl gave his criterion for uniform distribution (mod 1): a sequence {xn} is u. d. (mod 1) if and only if
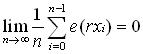
for positive integers r, where e(a) = e2πia. It implies that {nα} is u. d. (mod 1) if and only if α is irrational and is the basis for many other results.
The author says that the main questions that motivated his book are
Is there a transcendental real number α such that ‖αn‖ tends to 0 as n tends to infinity?
Is the sequence of fractional parts of {(3/2)n}, n ≥ 1, dense in the unit interval?
What can be said on the digital expansion of an irrational algebraic number?
The book contains ten chapters that are largely independent of each other, ending with a chapter of conjectures and open questions. See the table of contents for what is in the various chapters.
Many results, many of them recent, are given. Each chapter ends with interesting notes. There are exercises (no hints or answers provided) that should not be attempted by the faint of heart. The list of references contains seven hundred and fifty-one items.
This is not a book for the general mathematical reader, but specialists should find it of great value. As always with Cambridge Mathematical Tracts, the book is a delight to the eye. If there are any misprints I didn’t notice them.
In 1964 Woody Dudley proved that though {cos nθ} is not uniformly distributed (mod 1) for almost all θ, {f(n)cos nθ} is, where f is any function such that f(n) goes to infinity with n, no matter how slowly. It is his best theorem.
1. Distribution modulo one
2. On the fractional parts of powers of real numbers
3. On the fractional parts of powers of algebraic numbers
4. Normal numbers
5. Further explicit constructions of normal and non-normal numbers
6. Normality to different bases
7. Diophantine approximation and digital properties
8. Digital expansion of algebraic numbers
9. Continued fraction expansions and beta-expansions
10. Conjectures and open problems
A. Combinatorics on words
B. Some elementary lemmata
C. Measure theory
D. Continued fractions
E. Diophantine approximation
F. Recurrence sequences
References
Index.
- Log in to post comments




