Fractional Differentiation Inequalities

After dealing with first, second, third,… derivatives it is natural to ask if sense can be made of half-derivatives, or, more generally, of D^p for non-integer values of p, where D denotes the differentiation operator. As long ago as 1695 L’Hôpital and Leibniz corresponded on the subject. Leibniz said that the half-derivative “leads to a paradox” that he did not specify. Euler, who could do anything, showed that the half-derivative of x is  In the nineteenth century, Liouville worked on them, as have others since.

In the later twentieth century they became used in applications. I have seen papers in journals of electrical, civil, and mechanical engineering devoted to results on fractional derivatives. I don’t know enough about the subjects to be able to tell if the applications are practical or whether the engineers, captivated by the mathematics, are making contributions to the theory of their subject. In any event, fractional derivatives seem now to be a hot topic. I could say that they should be included in calculus textbooks, but I will not because I don’t want calculus texts to be any longer.

A natural way to get a handle on fractional derivatives is to take the nth derivative of an exponential,  and generalize it to non-integer values of n, so, setting n = 1/2 for example, the half-derivative of  is , which seems reasonable. The eth derivative of  is  which, if not especially reasonable, is at least picturesque. Differentiating we get

,

so

 and ,

also satisfyingly as they should be. Thus we can define fractional derivatives of functions that can be written as Fourier series.

However, x cannot be so written. Another idea is close to hand. Observing that

we go immediately to

for n an integer less than k and then immediately to

for any p less than k. Thus the half-derivative of x is .

Taking the half-derivative of that gives 1, as we would expect.

Now that we have fractional derivatives of powers of x we have fractional derivatives of functions that can be written as Taylor series. But look at what happens. Using its Taylor series, the half-derivative of  is

,

which does not look like the Taylor series for , the half-derivative of that we found before.

The reason why is interesting. When n is a negative integer, when we apply  we are performing integrations, which take place over an interval. It turns out that when we calculate  for p positive we are also performing an operation over an interval. However, when p is a positive integer the interval as it were collapses and we think, wrongly, that all derivatives are local phenomena. First derivatives are, but half-derivatives are not. The discrepancy in the half-derivatives for  arises from using different intervals, [0, x] for the Taylor series and  for the other. Could this have been the paradox that Leibniz saw? Possibly, though another is that  is not always the same as

Professor Anastassiou considers three definitions of fractional derivatives. One is the Riemann-Liouville fractional derivative

,

where m = [p] + 1. (The lower limit of the integral may be elsewhere than 0.) Another is the Caputo fractional derivative

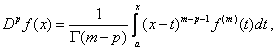
where . The Canavati fractional derivative is another variation.

His interest is in deriving inequalities for fractional derivatives, generalizations of

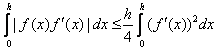
(where  and ) and other inequalities of Poincaré, Sobolev, Hilbert, Ostrowski, and others. They are, as he says, “expanded in all possible directions” in this 675-page book. I will not quote any of his many results, partly to save space: the statement of Theorem 15.82 takes up an entire page, less two lines.

Part of the length of the book is owing to the author’s wish to have each of its twenty-six chapters independent of all the rest, a good idea but one that leads to some repetition. The list of references runs to four hundred and twelve items. This is not a book for the general mathematical reader but I can imagine that for a specialist in fractional derivative inequalities it would be indispensible.

I suspect that the author’s first language was not English. His style does not always conform to customary idioms and sometimes brings the reader up short: “We must not overlook the great fractional calculus encyclopedic monograph by S. Samko, A. Kilbas, and O. Marichev [366], and supports which strongly all the above recent scientific activities.” The number of typographical errors is larger than I would expect to find in a Springer book and the index is feeble. I suspect that Springer skimped on editing but it is nevertheless to be congratulated for having the courage and enterprise to publish a book that it knows has only a small audience but publishing it anyway. That is admirable, as is the number and variety of the results that the book contains.

Woody Dudley has calculated very few derivatives since he retired in 2004, but he has not forgotten how to find them, fractional or otherwise.