- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Geometric Etudes in Combinatorial Mathematics

Publisher:
Springer
Publication Date:
2010
Number of Pages:
261
Format:
Paperback
Edition:
2
Price:
59.95
ISBN:
9780387754697
Category:
Monograph
The Basic Library List Committee recommends this book for acquisition by undergraduate mathematics libraries.
[Reviewed by , on ]
Alex Bogomolny
11/23/2010
The first edition of this book came out with warm recommendations from Paul Erdös, Branko Grünbaum, and Cecil Rousseau. Rousseau is among the 10 top Erdös coauthors. The Russian translation of Grünbaum's own Etudes in Combinatorial Geometry and in the Theory of Convex Sets was a bestseller among young mathematicians when it appeared in 1971, right when Alexander Soifer was an undergraduate student. (Among other accomplishments B. Grünbaum has distinguished himself by detecting in 1985 a defect in the geometry of the MAA logo that was introduced in 1972.) The first edition of the book received a glowing review from Don Chakerian (The American Mathematical Monthly, Vol. 99, No. 5 (May, 1992), pp. 486-489).
The second edition of the book features specially written Forewards by Grünbaum, Rousseau and Peter D. Johnson, Jr. Grünbaum wrote for the second edition:
Each time I looked at Geometric Etudes in Combinatorial Mathematics I found something new and surprising to me, even after more than fifty years working in combinatorial geometry.
For the second edition, A. Soifer added 5 relatively small chapters to the original four, and had upgraded the latter. The add-ons reflect the relevant developments since the appearance of the first edition of the book.
The first chapter is taken up with variations on the theme of tiling rectangles, cylinders, tori, and Möbius' bands with polyominoes and their 3D analogues. The add-on chapters 5 and 6 relate to that theme. Chapter 5 describes the 2005 results of Dmytro Karabash. Karabash first answered in the negative the following problem (5.3):
Is it true that an n×m rectangle is orientable if and only if one of the numbers n, m is divisible by 4, the other is even?
A rectangle is orientable if it can be tiled by L-tetrominoes of the same orientation. Karabash came up with the following counterexample:
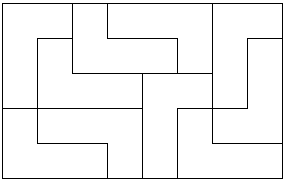
He also proved that an n×m rectangle is orientable if and only if 8|mn and neither of n, m equals 1 or 3.
Chapter 6 presents Norton Starr's result on tiling of a n×n×n cube with 3D L-trominoes and monominoes (plain cubes). For n ≡ 1 (mod 3), the cube is tiled with L-trominoes and 1 monomino. For n ≡ 2 (mod 3), the cube is tiled with L-trominoes and 2 monominoes. In both cases, the monominoes can be placed anywhere in the cube.
The second chapter of the book introduces the Pigeonhole principle. Here is a tasteful pair of exercises:
(7.3) Prove that among any nine points inside or on the boundary of a triangle of area 1, there are three points that form a triangle of area not exceeding 1/4.
(7.4) Prove that among any seven points inside or on the boundary of a triangle of area 1, there are three points that form a triangle of area not exceeding 1/4.
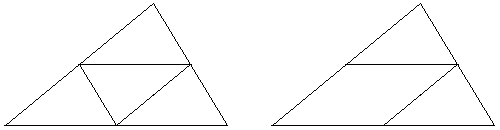
While (7.3) is solved with the 4-way partition of the triangle by its midlines, the solution for (7.4) has one of the midlines missing. In case three out of seven given points fall into the parallelogram, one needs to prove that a triangle within a parallelogram of area 1/2 may at most have the area of 1/4.
The second part of Chapter 2 extends the pigeonhole principle to infinite sets: if an infinite flock of pigeons lands on a finite number of holes, then at least one hole contains an infinite number of pigeons. In this form, the pigeonhole helps prove the Bolzano-Weierstrass theorem in R and Rn and, subsequently, in the space of compact subsets of the plane furnished with the Hausdorff metric. This serves a tool to close the gaps in Jacob Steiner's proof of the Isoperimetric theorem.
Chapter 3 offers an introduction to the graph theory, Ramsey numbers, graph planarity. With a nice touch, Soifer connects the tiling of graphs with graphs and the tiling of rectangles with polyominoes from Chapter 1. This is followed by a discussion of Kuratowski's criterion of planarity, comparison of the crossing and rectilinear crossing numbers in 2D and 3D, Euler's formula, and a proof of Jordan Curve Theorem for polygonal curves.
Chapter 7 chronicles the events surrounding B. D. McKay and S. P. Radziszowski's establishment (1993) of the exact value of the Ramsey number R(4, 5), viz., R(4, 5) = 25.
Chapter 4, by far the largest in the book, deals with various questions from the theory of convex sets. A short introduction is followed by Blaschke's theorem with immediate applications and Borsuk's theorem and conjecture. Borsuk's number a(F) of a bounded figure F ⊂ R is the smallest of the integers s for which there is a decomposition of F into s figures of smaller diameter. Karol Borsuk asked in 1933 whether a(F) ≤ n + 1, for F ⊂ Rn. He proved the conjecture for n = 2. H. G. Eggleston (1955) showed it is true for n = 3.
Chapter 8 reports on the most recent results concerning Borsuk's conjecture. It was disproved in 1993 by Jeff Kahn and Gil Kalai, who published a counterexample in R1326. The current record is a 2002 result disproving the conjecture in 298 dimensions!
Chapter 4 continues with the properties of plane figures of constant width and Barbier's theorem in particular. V. Boltyanski's theorem asserts that, in the plane, a(F) = 3 only if there is unique figure of constant width of the least diameter containing F. a(F) = 2, otherwise. A very recent proof of Borsuk's theorem is due to K. Kolodziejczyk. Before turning to the Helly and Szökefalvi-Nagy theorems, the chapter covers H. Hadwiger's illumination and covering problems (of a figure with smaller copies of itself.)
Chapter 9 introduces a genuinely new topic unrelated to the first edition of the book: the chromatic number of the plane and its relatives. If a plane is colored with three colors, there is always a monochromatic pair of points one unit apart. If 4 colors are used a monochromatic pair may or may not exist. With 7 colors one may ensure non-existence of a monochromatic pair. The least such number is denoted χ and called the chromatic number of the plane. 4 ≤ χ ≤ 7. Both bounds have been established in 1950.
In the definition of χ, a unit length is forbidden for all colors. If it's forbidden for all colors but one, the new chromatic number is denoted χa: 4 ≤ χa ≤ 6. The polychromatic number χp answers P. Erdös' question: What is the smallest number of colors needed to color the plane so that no color realizes all distances? D. E. Raiskii's theorem (1970) states that again 4 ≤ χp ≤ 6.
Characteristically, each of the topics included in the book require very little in the way of preparation and quickly evolve into open questions and research-level conjectures. Each of the first 4 chapters is divided into sections organized as a sequence of exercises leading to an important result. Each section includes solutions to the exercises. The book continues the tradition of such classics as the 1965 Results and Problems in Combinatorial Geometry by V. G. Boltyanski and I. Z. Gohberg and the 1964 Combinatorial Geometry in the Plane by H. Debrunner and H. Hadwiger. This is a delightful book that will be welcomed enthusiastically by students and organizers of mathematical circles and mathematics fans.
Alex Bogomolny is a freelance mathematician and educational web developer. He regularly works on his website Interactive Mathematics Miscellany and Puzzles and blogs at Cut The Knot Math.
See the table of contents in pdf format.
- Log in to post comments




