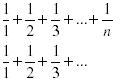- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Math Girls

Publisher:
Bento Books
Publication Date:
2011
Number of Pages:
288
Format:
Paperback
Price:
14.99
ISBN:
9780983951308
Category:
General
[Reviewed by , on ]
Marion Cohen
02/16/2012
Imagine the improbable: high-school students getting together on their own — not in a Math Club or Math Circle, not in preparation for any Math Olympiad or “regular” test, not on the advice of any of their teachers, not as part of any organized program — to talk about pure math, math more interesting than the math found in their textbooks. The three students in this book do that for the sheer love of it. That to me is the beauty and fascination of this novel for young people, mostly young people interested in math. The publishers call it “Glee for math geeks”.
On page 4 the narrator, the sole male among the three students, remaining nameless throughout the book, writes about his first day of high school.
Back in class everyone would be introducing themselves. I hated introductions. What was I supposed to say?
“Hi. My hobbies include math and… uh… Well, mostly just math…” I had resigned myself to the idea that high school would turn out much as middle school had. Three years of patiently sitting through classes. Three years with my equations in a quiet library.
Ah, but fast-forward a minute or two and
A girl stood in front of [a particularly large cherry tree], admiring the blossoms…She looked at me. She was tall, with long black hair brushed back from metal frame glasses… “One, one, two, three,” she said… she stopped and pointed in my direction, obviously waiting for the next number.
The narrator quickly names the next Fibonacci number, but almost immediately the girl virtually snaps, “1, 4, 27, 256…”, then a still harder sequence to find a pattern of. Thus begins the narrator’s friendship with, as the author puts it (p. 1), “the brilliant Miruka, forever stunning me with her elegant solutions”. His second year of high school brings on a friendship with another “math girl” — (p. 1) “the vivacious Tetra, with her earnest stream of questions”. “We went to the same junior high,” begins her letter to our narrator. “I’m one year behind you. I’m writing to ask you for some advice about studying math… do you think you could spare the time to talk?”
At first the two math friendships are disjoint. Miruka is, at least apparently, better at math than our narrator while Tetra is, apparently, worse. Eventually the twain — or rather, the trio — meet. Miruka comes upon the other two in the library, and she’s jealous and behaves like a “mean girl”. That competition goes on for awhile, the two math friendships remaining disjoint, but eventually — via a math problem, more specifically a question that is Tetra’s and Tetra’s alone — Miruka acquires respect for Tetra and the two become friends. Or rather, the three become friends.
One might remark that the main character of this book is math. At any rate, math takes up the most space. If one opens to almost any page, one finds, usually on the entire page, math, complete with symbols. Often the math is indistinguishable from the math in a math text, except for the quotation marks because the math is spoken (or written) by one of the three friends (usually Miruka). “Sometimes the math goes over your head — or at least my head,” writes Daniel Pink in a blurb for the book. “But that hardly matters. The focus here is the joy of learning, which the book conveys with aplomb.” Also, sometimes the math is not indistinguishable from the math in a text. We’re aware that it’s being explained or discussed by the three friends, and sometimes the pedagogy, usually Miruka’s, is something teachers would do well not to forget. For example (p. 119),
“Writing everything out just made it harder to see the pattern, so I tidied everything up, using sigma notation” and (p. 143),
Take a look at these two expressions:
Both of them have an ellipsis, right? But the meaning is a little bit different. Do you see which one means “infinity”?
Other times we’re made aware that this is a conversation among the three friends via questions being asked, usually by Tetra. (p. 153) “…What’s the M in that inequality, anyway?” Or ruminations, again by Tetra. (p. 142) “Hmm. I’m not sure I got all that, but I did get the part about figuring out what an is when n is really, really big.”
Sometimes this throwing in of “ordinary non-math” conversation felt contrived to me; why not just do the math?, I thought. One quote that went against my grain appears on p. 180. “A beautiful proof, isn’t it?” says Miruka. ”It was passed down to us from the master.” Personalities differ, and the setting of this book is Japan, but I can’t imagine a teenager speaking in that way, both the “beautiful” and the “master”. As a teenager I certainly believed that math was beautiful but I would never have expressed it that way. And I was not mature enough, nor emotionally ready, to appreciate any “master”. But non-math conversation there needs to be in a novel. It also serves as an ingenious device to both slow down the math and present it in a way that someone learning it will be able to follow. And, of course, to add interest, sometimes romantic interest.
The book is said to be a best-seller in Japan. I heard in a short review on YouTube that, in that country, there are math groups focused on that book and, I assume, taking off from there. The reviewers — Joanne Manaster and her teen-aged daughter — express their hope that the same will happen in the US.
The math appearing in the book includes an expression for the sum of the divisors of a number when given its prime factorization, complex numbers, De Moivre’s formula, a closed-form expressions for the nth Fibonacci number (found using the idea of generating function), the arithmetic-geometric mean inequality, (p. 89) “the discrete world vs. the continuous world”, Catalan numbers, the infinite harmonic series, and something I’d never heard of (or not using that term) called “the falling factorial” — It’s x(x–1)(x-2)… with n factors — and its extension for non-positive n, calculus (to some extent) along with Maclaurin series, a proof (found jointly by the three friends) that
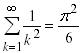 ,
,
and finally results towards finding a formula for the partition number of n.
Sometimes more than one way of finding or proving something is given. Sometimes “bargain information” is obtained along the way. We often find interesting revelations about math and doing math, though usually new only to young people. Spoken by Miruka (p. 252) after our narrator finds an interesting method that doesn’t work for the problem at hand:
You’re hardly the first mathematician to go down the wrong path. But you know what? If you don’t go looking you’ll never know what you might have found. If you don’t try new things, you’ll never know what you’re capable of. We’re on a journey here. Sometimes we get tired, and sometimes we get lost. But that’s no reason to give up.”
And soon, “Maybe it didn’t help with this problem… but I bet it would help somewhere else.” And on page 1 the narrator gives his contribution to the “Mathematics is” sidebars in the Monthly.
Mathematics is ageless.
Through equations, I can share the experiences of mathematicians from ages past. They might have worked their proofs hundreds of years ago, but when I trace the path of their logic, the thrill that fills me is mine.
Mathematics leads me into deep forests and reveals hidden treasures. It’s a competition of intellect, a thrilling game where finding the most powerful solution to a problem is the goal. It is drama. It is battle…
When I read a book I usually ask myself in what ways I identify with it or with any of the characters. I had to think twice with this one. On the one hand, like the narrator, in high school I was more or less a math loner (though not a loner in every sense; I had friends with whom I did other things, and I had other interests — for example classical piano, like Miruka). But there were two differences between the book’s narrator and me. First, I liked being a math loner; I liked, at least during that period in my life, having math all to myself. I had my own private math ideas, some of which amounted to something, some of which didn’t. (One developed, over fifty years, into a paper I just finished and submitted.) I’m not sure I would have liked discovering other math loners to stop being math loners with. Not just yet. Second, the math that I did was different from the math in this book. I didn’t specifically aim for college-level math, in particular calculus. I would browse in the math department of the larger bookstores, mostly Barnes and Noble, and whatever math grabbed me, I grabbed back. What I remember is Gödel’s proof, transfinite numbers, and in general more abstract ideas, rather than the number theory and other concrete calculations appearing in this book.
That last paragraph is not meant as a criticism of the book. It is only meant to say that there are many ways in which budding mathematicians can relate to math in satisfactory ways, and in which they eventually also use their love of math to connect with other human beings. I admit that the book did make me wonder: What if, in high school, I had discovered another student or students who, not only got As in math, but loved and pursued math as I did?
One might quibble with the title, “Math Girls”, and also with the character of Miruka — a bit nervy, and aggressive rather than assertive — and with the fact that the narrator is a guy. A woman — well, this woman — might ask the question, “What would such a book be like if it were told from the point of view of Miruka or Tetra?”
A book of this sort can’t be easy to translate, and the translator, Tony Gonzalez, was usually up to the task, keeping the math correct and the charm of the book intact. There were less than a handful of exceptions, which could also have been due to the author. On p. 56, “I want to represent Fn as a closed equation…”? And p. 27, “An equation is a statement that’s true when you replace the xs with a certain number. An identity is a statement that’s true when you replace the xs with any number.” To me an equation is anything with an equal sign (including identities). Some equations need to be solved. Identities don’t.
One exceptional teacher in the book took an interest in the math threesome and intervened in a minimally invasive and effective way. Still, I’d like to end this review with a quote by the book’s author:
If you’re learning something because you enjoy it, you can’t let something like school hold you back. Study as deep, as wide, and as far as you can.
Food for thought, and perhaps good advice for certain students. One might also say that it expresses the spirit of the book.
Marion Cohen teaches math at Arcadia University in Glenside, PA. She is the author of Crossing the Equal Sign, a poetry book about the experience of math.
The table of contents is not available.
- Log in to post comments