- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Who's #1? — The Science of Rating and Ranking

Publisher:
Princeton University Press
Publication Date:
2012
Number of Pages:
266
Format:
Hardcover
Price:
29.95
ISBN:
9780691154220
Category:
General
The Basic Library List Committee suggests that undergraduate mathematics libraries consider this book for acquisition.
[Reviewed by , on ]
Richard J. Wilders
03/29/2012
As most anyone with even a passing interest in sports is aware, sports rankings are now a virtual obsession with the media. Since rankings are subject to mathematical analysis, many mathematicians (and others) have constructed ranking systems of widely varying credibility. From the widely disparaged BCS ratings in college football to the latest Vegas line, ratings and their associated rankings are everywhere. Besides the big business of college sports, Netflix also uses a ratings system to rate its films. They awarded a $1 million prize to a team who improved their ratings system by 10%. And, of course, there is the Google page ranking system, the subject of an earlier book, Google’s PageRank and Beyond: The Science of Search Engine Rankings, by the same authors. Who’s #1 provides a fascinating tour through the world of rankings and is highly recommended.
To be clear before we delve into the details: a rating system assigns a number to each of a set of teams. Those same teams can then be ranked (1st, 2nd, …) based on their numerical rating. The BSC system assigns a decimal between 0 and 1 to each team in its rating universe. Ranking is then computed by ranking the team with the highest BSC rating as #1 and then moving down the line. Ranking can be done by a voting system (also part of the BCS ranking system) but such voting schemes are subject to Arrow’s results and thus never certain to produce results which satisfy even minimal conditions such a voting scheme ought to satisfy (pages 3–4).
Who’s # 1 provides a generous sampling of the various ways to construct a rating system as well as an analysis of the strengths and weaknesses of each of them. There are several examples used throughout. Here’s one of them: how would you rate these 5 football teams based on their performance against each other?
|
|
Duke |
Miami |
UNC |
UVA |
VT |
Record |
Point Differential |
|
Duke |
|
7-52 |
21-24 |
7-38 |
0-45 |
0-4 |
–124 |
|
Miami |
52-7 |
|
34-16 |
25-17 |
27-7 |
4-0 |
91 |
|
UNC |
24-21 |
16-31 |
|
7-5 |
3-30 |
2-2 |
–40 |
|
UVA |
38-7 |
17-25 |
5-7 |
|
14-52 |
1-3 |
–17 |
|
VT |
45-0 |
7-27 |
30-3 |
52-14 |
|
3-1 |
90 |
(Baffled by the initials? UNC = University of North Carolina, UVA = University of Virginia, and VT = Virginia Tech.)
There are two obvious ways to rate the teams: win-loss record and total point differential. These yield the following ratings and associated rankings:
|
|
Wins |
Point Diff |
|
|
Wins |
Point Diff |
|
Miami |
4 |
91 |
|
Miami |
4 |
91 |
|
VT |
3 |
90 |
|
VT |
3 |
90 |
|
UNC |
2 |
–40 |
|
UVA |
1 |
–17 |
|
UVA |
1 |
–17 |
|
UNC |
2 |
–40 |
|
Duke |
0 |
–124 |
|
Duke |
0 |
–124 |
While the two ratings agree on 3 of the 5 teams, the point differential reverses the ranking for UVA and UNC. Even though UNC won 2 games and UVA won only 1, UVA lost by a smaller overall margin. However, a closer analysis reveals this was due mostly to the fact that UVA beat Duke by 31 points while UNC beat Duke by only 3. Perhaps UVA ran up the score against the hapless Blue Devils and we shouldn’t give them so much credit for that? The issue of point differential and the presumed evil of teams running up the score against weaker opponents surfaces again and again as various rating schemes are considered.
Just how different are these two rankings? Chapter 16 investigates just that topic — the quantitative measure of concordance/discordance among two ranked lists. The simplest (assuming both lists contain the same teams/items) is the Kendall Tau (page 204):
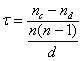
Here nc represents the number of times two teams are ranked the same in each list, while nd represents the number of times the rankings differ (in either direction). The denominator represents the total number of such comparisons and hence –1 ≤ τ ≤ 1, with 1 representing perfect agreement and –1 representing complete disagreement. In our example, τ = .8. Needless to say, this is not all that can be said about such comparisons — consult chapter 16 for the details.
Each chapter presents one or more seemingly plausible ratings systems along with a bit of history concerning their creation. Here are two examples.
Massey Rating System
Created in 1997 by Kenneth Massey as part of his honors thesis at Bluefield College, this rating is one of those used in the BCS ratings scheme. In its simple form, the Massey systems uses least squares analysis to find a set of ratings ri with the property that the difference in ratings predicts the margin of victory/defeat when team i plays team j (ri – rj = yk). We thus start with a matrix equation of the from Xr = y, where the margins of victory are known (for games already played) and we are seeking to find a least squares solution for vector r. This is overdetermined and inconsistent so Massey solves the normal equation XTXr = XTy. Adding the constraint that the sum of all ranks must be 0 yields the following Massey Rating for our intrepid ACC football rivals:
|
|
Rating |
Rank |
|
Miami |
18.2 |
1 |
|
VT |
18 |
2 |
|
UNC |
–3.4 |
3 |
|
UNC |
–8 |
4 |
|
Duke |
–24.8 |
5 |
Massey added an additional wrinkle by creating offensive and defensive rankings for each team; a system which allows Duke to crawl out of the cellar in one category by placing 4th in Offensive Ranking. For more on Massey consult Who’s #1? or google “Massey.” The remainder of the chapter outlines the other components of the BSC formula including the Notre Dame rule. See page18 for details.
Chess and the NFL: The Elo Rating System
From college football we move to chess — where rankings carry less monetary but significantly greater political significance. Those of us who were alive when Bobby Fisher was at his peak recall that a drop in his ranking was considered tantamount to our losing the cold war. The method discussed was created by Arpad Elo, a physics professor at Marquette University. His notion was to treat a player’s performance as a normally distributed random variable X whose mean µ changes only very slowly after a player’s game is established. As the system was implemented it was discovered that performance is not generally normally distributed. The current system assumes that expected scoring difference between two players is a logistic function of their ratings.
Langville and Meyer complete the chapter on Elo ratings with an analysis of the 2009–2010 National Football League season. With full season data, the Elo ratings correctly predict (hindsight accuracy) 75.3% of all games. Computing the Elo ratings as the season progressed yields a foresight accuracy of 62.2%. That’s pretty good, but winning at Vegas requires not just picking the winner, but the margin of victory — for that analysis proceed to chapter 9!
I would recommend this book for any college library. It’s a great source of projects for students at all levels. Beginning students could try some of the schemes on their local athletic conference while advanced students could attempt to add to the collection of ratings schemes and dream of saving (or destroying) the BCS.
Richard Wilders is Marie and Bernice Gantzert Professor in the Liberal Arts and Sciences and Professor of Mathematics at North Central College. His primary areas of interest are the history and philosophy of mathematics and of science. He has been a member of the Illinois Section of the Mathematical Association of America for 30 years and is a recipient of its Distinguished Service Award. His email address is rjwilders@noctrl.edu.
Preface xiii
Purpose xiii
Audience xiii
Prerequisites xiii
Teaching from This Book xiv
Acknowledgments xiv
Chapter 1. Introduction to Ranking 1
Social Choice and Arrow's Impossibility Theorem 3
Arrow's Impossibility Theorem 4
Small Running Example 4
Chapter 2. Massey's Method 9
Initial Massey Rating Method 9
Massey's Main Idea 9
The Running Example Using the Massey Rating Method 11
Advanced Features of the Massey Rating Method 11
The Running Example: Advanced Massey Rating Method 12
Summary of the Massey Rating Method 13
Chapter 3. Colley's Method 21
The Running Example 23
Summary of the Colley Rating Method 24
Connection between Massey and Colley Methods 24
Chapter 4. Keener's Method 29
Strength and Rating Stipulations 29
Selecting Strength Attributes 29
Laplace's Rule of Succession 30
To Skew or Not to Skew? 31
Normalization 32
Chicken or Egg? 33
Ratings 33
Strength 33
The Keystone Equation 34
Constraints 35
Perron-Frobenius 36
Important Properties 37
Computing the Ratings Vector 37
Forcing Irreducibility and Primitivity 39
Summary 40
The 2009-2010 NFL Season 42
Jim Keener vs. Bill James 45
Back to the Future 48
Can Keener Make You Rich? 49
Conclusion 50
Chapter 5. Elo's System 53
Elegant Wisdom 55
The K-Factor 55
The Logistic Parameter ? 56
Constant Sums 56
Elo in the NFL 57
Hindsight Accuracy 58
Foresight Accuracy 59
Incorporating Game Scores 59
Hindsight and Foresight with ? = 1000, K = 32, H = 15 60
Using Variable K-Factors with NFL Scores 60
Hindsight and Foresight Using Scores and Variable K-Factors 62
Game-by-Game Analysis 62
Conclusion 64
Chapter 6. The Markov Method 67
The Markov Method 67
Voting with Losses 68
Losers Vote with Point Differentials 69
Winners and Losers Vote with Points 70
Beyond Game Scores 71
Handling Undefeated Teams 73
Summary of the Markov Rating Method 75
Connection between the Markov and Massey Methods 76
Chapter 7. The Offense-Defense Rating Method 79
OD Objective 79
OD Premise 79
But Which Comes First? 80
Alternating Refinement Process 81
The Divorce 81
Combining the OD Ratings 82
Our Recurring Example 82
Scoring vs. Yardage 83
The 2009-2010 NFL OD Ratings 84
Mathematical Analysis of the OD Method 87
Diagonals 88
Sinkhorn-Knopp 89
OD Matrices 89
The OD Ratings and Sinkhorn-Knopp 90
Cheating a Bit 91
Chapter 8. Ranking by Reordering Methods 97
Rank Differentials 98
The Running Example 99
Solving the Optimization Problem 101
The Relaxed Problem 103
An Evolutionary Approach 103
Advanced Rank-Differential Models 105
Summary of the Rank-Differential Method 106
Properties of the Rank-Differential Method 106
Rating Differentials 107
The Running Example 109
Solving the Reordering Problem 110
Summary of the Rating-Differential Method 111
Chapter 9. Point Spreads 113
What It Is (and Isn't) 113
The Vig (or Juice) 114
Why Not Just Offer Odds? 114
How Spread Betting Works 114
Beating the Spread 115
Over/Under Betting 115
Why Is It Difficult for Ratings to Predict Spreads? 116
Using Spreads to Build Ratings (to Predict Spreads?) 117
NFL 2009-2010 Spread Ratings 120
Some Shootouts 121
Other Pair-wise Comparisons 124
Conclusion 125
Chapter 10. User Preference Ratings 127
Direct Comparisons 129
Direct Comparisons, Preference Graphs, and Markov Chains 130
Centroids vs. Markov Chains 132
Conclusion 133
Chapter 11. Handling Ties 135
Input Ties vs. Output Ties 136
Incorporating Ties 136
The Colley Method 136
The Massey Method 137
The Markov Method 137
The OD, Keener, and Elo Methods 138
Theoretical Results from Perturbation Analysis 139
Results from Real Datasets 140
Ranking Movies 140
Ranking NHL Hockey Teams 141
Induced Ties 142
Summary 144
Chapter 12. Incorporating Weights 147
Four Basic Weighting Schemes 147
Weighted Massey 149
Weighted Colley 150
Weighted Keener 150
Weighted Elo 150
Weighted Markov 150
Weighted OD 151
Weighted Differential Methods 151
Chapter 13. "What If . . ." Scenarios and Sensitivity 155
The Impact of a Rank-One Update 155
Sensitivity 156
Chapter 14. Rank Aggregation-Part 1 159
Arrow's Criteria Revisited 160
Rank-Aggregation Methods 163
Borda Count 165
Average Rank 166
Simulated Game Data 167
Graph Theory Method of Rank Aggregation 172
A Refinement Step after Rank Aggregation 175
Rating Aggregation 176
Producing Rating Vectors from Rating Aggregation-Matrices 178
Summary of Aggregation Methods 181
Chapter 15. Rank Aggregation-Part 2 183
The Running Example 185
Solving the BILP 186
Multiple Optimal Solutions for the BILP 187
The LP Relaxation of the BILP 188
Constraint Relaxation 190
Sensitivity Analysis 191
Bounding 191
Summary of the Rank-Aggregation (by Optimization) Method 193
Revisiting the Rating-Differential Method 194
Rating Differential vs. Rank Aggregation 194
The Running Example 196
Chapter 16. Methods of Comparison 201
Qualitative Deviation between Two Ranked Lists 201
Kendall's Tau 203
Kendall's Tau on Full Lists 204
Kendall's Tau on Partial Lists 205
Spearman's Weighted Footrule on Full Lists 206
Spearman's Weighted Footrule on Partial Lists 207
Partial Lists of Varying Length 210
Yardsticks: Comparing to a Known Standard 211
Yardsticks: Comparing to an Aggregated List 211
Retroactive Scoring 212
Future Predictions 212
Learning Curve 214
Distance to Hillside Form 214
Chapter 17. Data 217
Massey's Sports Data Server 217
Pomeroy's College Basketball Data 218
Scraping Your Own Data 218
Creating Pair-wise Comparison Matrices 220
Chapter 18. Epilogue 223
Analytic Hierarchy Process (AHP) 223
The Redmond Method 223
The Park-Newman Method 224
Logistic Regression/Markov Chain Method (LRMC) 224
Hochbaum Methods 224
Monte Carlo Simulations 224
Hard Core Statistical Analysis 225
And So Many Others 225
Glossary 231
Bibliography 235
Index 241
- Log in to post comments




