- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The College Mathematics Journal - May 2005
May 2005 Contents
ARTICLES
On the Way to "Mathematical Games": Part I of an Interview with Martin Gardner
Don Albers
178-190
In this portion of the interview, Martin Gardner discusses his childhood, education, military service, and the beginnings of his career in writing.
M&m Sequences
Harris S. Schultz and Ray C. Shiflett
191-198
Consider a sequence recursively formed as follows: Start with three real numbers, and then when k are known, let the (k +1)st be such that the mean of all k +1 equals the median of the first k. The authors conjecture that every such sequence eventually becomes stable. This article presents results related to their conjecture.
If 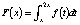 Is Constant, Must f (t ) = c / t ?
Is Constant, Must f (t ) = c / t ?
Tian-Xiao He, Zachariah Sinkala, and Xiaoya Zha
199-204
The familiar property of integral of  led to the discovery of other functions with this property.
led to the discovery of other functions with this property.
Intersections of Tangent Lines of Exponential Functions
Timothy G. Feeman and Osvaldo Marrero
205-208
This article looks at how a particular curve associated with tangents of an exponential function is a copy of the exponential itself.
The Probability that an Amazing Card Trick Is Dull
Christopher Swanson
209-212
The author describes a card trick that failed when he tried it with the student chapter at his university. Computations show that the chance of this happening is about 1 in 25.
Making a Bed
Anthony Wexler and Sherman Stein
213-221
The origins of this paper lay in making beds by putting pieces of plywood on a frame: If beds need to be 4 feet 6 inches by 6 feet 3 inches, and plywood comes in 4-foot by 8-foot sheets, how should one cut the plywood to minimize waste (and have stable beds)? The problem is of course generalized.
Fallacies, Flaws, and Flimflam
Ed Barbeau, editor
222-223
Classroom Capsules
Michael Kinyon, editor
224-237
A Geometric Series from Tennis
James Sandefur
224-226
In this note, a formula is found, using geometric series, for the probability that a player wins from deuce (by the required two points) given a fixed probability p of winning each point.On Sums of Cubes
Hajrudin Fejzic, Dan Rinne, and Bob Stein
226-228
The sums of cubes discussed here are modifications of the well known identitySymmetry at Infinity
Jennifer Switkes
228-231
The symmetry in the title arises in the centers of masses of some plane laminas.The Flip-Side of a Lagrange Multiplier Problem
Angelo Segalla and Saleem Watson
232-235
The "flip-side" of an optimization problem is dual in the way that maximizing the area of a rectangle with given perimeter corresponds to minimizing the perimeter for fixed area. This note looks at this duality from a Lagrange multiplier perspective.Another Proof for the p-Series Test
Yang Hansheng and Bin Lu
235-237
The proof presented here is an alternative to the integral test that is usually used.
Problems and Solutions
Media Highlights
Book Review
A Mathematician at the Ballpark by Keith Devlin





