- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The College Mathematics Journal - May 2006
ARTICLES
Complementary Coffee Cups
Thomas Banchoff
170-175
What may have been the birth of a new calculus problem took place when the author noticed that two coffee cups, one convex and one concave, fit nicely together, and he wondered which held more coffee. The fact that their volumes were about equal led to the topic of this article: complementary surfaces of revolution with equal volumes.
Folding Beauties
Leah Wrenn Berman
176-186
This article has its genesis in an MAA mini-course on origami, where a way to get a parabola by folding paper was presented. This article discusses the methods and mathematics of other curves obtained by paper-folding.
Synchronizing Fireflies
Ying Zhou, Walter Gall, and Karen Mayumi Nabb
187-193
"Imagine a tenth of a mile of river front with an unbroken line of trees with fireflies on ever leaf flashing in synchronism. ... Then, if one's imagination is sufficiently vivid, he may form some conception of this amazing spectacle." So wrote the naturalist Hugh Smith. In this article we consider how one might model mathematically the synchronization between two fireflies using a system of differential equations that represent two coupled biological clocks with sine and square-wave interactions.
From Chebyshev to Bernstein: A Tour of Polynomials Small and Large
Matthew Boelkins, Jennifer Miller, and Benjamin Vugteveen
194-204
Consider the family of monic polynomials of degree n having zeros at -1 and +1 and all their other real zeros in between these two values. This article explores the size of these polynomials using the supremum of the absolute value on [-1, 1], showing that scaled Chebyshev and Bernstein polynomials give the extremes.
The Tippy Trough
Donald Francis Young
205-213
Consider a trough with a uniform cross section that is bounded by different functions on its two sides, and assume that the trough can be tipped either way. The question explored is this: If the trough is partially filled with water, what angle of tipping will maximize the depth of the water?
Fallacies, Flaws, and Flimflam
Ed Barbeau, editor
214-217
CAPSULES
Michael Kinyon, editor
218-228
Revisited: arctan 1 + arctan 2 + arctan 3 = π
Michael W. Ecker
218-219
A "three-fold" construction is given for constructing the angles on the left side of the identity. The geometry of the construction is then used to prove the identity.
A Bug Problem
Aaron Melman
219-221
The following problem is the topic of this capsule: a bug is on the inside of a container that has the shape of the paraboloid y = x2 revolved about the y-axis. If a liquid is poured into the container at a constant rate, how fast does the bug have to crawl to stay dry?
Streaks and Generalized Fibonacci Sequences
Shahla Ahdout, Sheldon Rothman, and Helen Strassberg
221-223
A sequence of n outcomes of successes and failures is called an n-string and a sequence of k successes in a row is a k-streak. It is shown that the number of n-strings that contain a 2-streak involves the Fibonacci numbers, and that this can be generalized to k-streaks.
The Non-Attacking Queens Game
Hassan Noon and Glen Van Brummelen
223-227
Gauss found a solution to the problem (first posed by Max Bezzel in 1848) of placing n queens on an n × n chessboard so that no queen is attacked by another. The nalfaro-queens game considered here is this: Two players alternately place queens on a board so that no two attack one another, and the winner is the player who places a queen so that all squares are attacked.
The Existence of Multiplicative Inverses
Ricardo Alfaro and Steven Althoen
227-228
Using only basic ideas from linear algebra and number theory (rather than the customary quotient fields and algebraic extensions), the authors show that if c is square-free, the ring 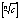 is a field.
is a field.




