The College Mathematics Journal Contents November 2008

Vol. 39, No. 5, pp. 330-427

ARTICLES

Leftist Numbers
Andrew Rich
330-336
The leftist number system consists of numbers with decimal digits arranged in strings to the left, instead of to the right. This system fails to be a field only because it contains zero-divisors. The same construction with prime base yields the p-adic numbers.

Report from the Ambassador to Cida-2
Clifton Cunningham
337-345
An interesting number system is developed in the context of an encounter with alien culture. The resulting system has intriguing parallels and contrasts with our real number system.

You Can Teach an Old Magician New Tricks
John P. Bonomo
346-356
Mathematics forms the basis for many types of card tricks. One of the best-known works as follows: Take any 15 cards out of a deck and ask a volunteer to select one of the cards and place it back in the deck. After shuffling the cards, you deal out three piles of cards and ask the volunteer which pile his or her card is in. You collect up the three piles and repeat this deal/collect procedure twice more and then magically select the volunteer's card from the deck. You can find many variations and analyses of this trick in various magic books and at several websites, using anywhere from 15 to 27 cards. Our purpose here is to analyze this trick in a manner which leads to two nice modifications of the trick. The first modification allows you to place the card in any location in the deck, and the second gives the volunteer full "control" over the trick: he/she deals out the cards as well as picks up the piles (in any order that they like). Even with this lack of control, the magician can pick the card correctly 87% of the time on the first try, and 100% on the second try. We then show how we can extend this trick to larger number of piles and cards.

Sets That Contain Their Circle Centers
Greg Martin
357-366
Say that a subset S of the plane is a "circle-center set" if S is not a subset of a line, and whenever we choose three non-collinear points from S, the center of the circle through those three points is also an element of S. A problem appearing on the Macalester College Problem of the Week website stated that a finite set of points in the plane, no three lying on a common line, cannot be a circle-center set. Various solutions to this problem that did not use the full strength of the hypotheses appeared, and the conjecture was subsequently made that every circle-center set is unbounded. In this article, we show how to prove a stronger assertion, namely that the one closed circle-center set is the entire plane, or equivalently that every circle-center set is dense in the plane. The step-by-step journey proceeds using elementary geometry for the most part, with a dash of plane topology thrown in.

Tuning with Triangles
Leon Harkleroad
367-373
This paper examines three historical geometric constructions for handcrafting stringed instruments. Using elementary geometry - in particular, triangles - these methods can provide quite good rational approximations to the irrationals that arise from tuning instruments in equal temperament. Interestingly, continued fractions help explain the accuracy of all approximations.

Variations of the Sliding Ladder Problem
Stelios Kapranidis and Reginald Koo
374-379
This article takes another look at the sliding ladder problem that students meet in the study of related rates in calculus. Physically realistic situations with both constrained and understrained ladders are explored.

CAPSULES

Sam Loyd's Courier Problem with Diophantus, Pythagoras, and Martin Gardner
Owen O'Shea
387-391
In Sam Loyd's classical Courier Problem, a courier goes around an army while both travel at constant speeds. If the army travels its length during the time the courier makes his trip, how far does the courier ride? In both revisions of this problem, a single-file army and a square army, the solution is irrational. Here, variations are considered in which the solutions are rational.

Beyond the Basel Problem
Lawrence Downey, Boon W. Ong, and James A. Sellers
391-394
Infinite sums of reciprocals of certain figurate numbers are often discussed in a first-year calculus course. For example, the sum of the reciprocals of the triangular numbers is easily determined since this is an example of a telescoping series. Moreover, the exact value of the sum of the reciprocals of the squares is often mentioned in such courses (with the exact value being 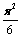). Unfortunately, little appears in the literature about sums of reciprocals of figurate numbers with more than four sides. Our goal in this capsule is to obtain a closed formula for all such infinite series where the number of sides of the figurate numbers is even and at least six.

An Elementary Trigonometric Equation
Victor H. Moll
394-399
The equation, 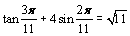is a classical example of the trigonometric equation A tan a + B sin b = C. This note provides a systematic study of this equation.

The Probability that Two Semigroup Elements Commute Can be Almost Anything
Berit Givens
399-400
The title indicates the content of this capsule. Among all finite semigroups, the set of probabilities that two elements commute is dense in [0, 1]. (This is in contrast to the fact that the corresponding probability for a non-Abelian group is never greater than 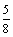).