- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
A Euclidean Approach to the FTC - Gregory's Proof of the FTC
This Euclidean definition of the tangent is pivotal to Gregory's contradiction. For if KC is not tangent to OEK, it means that some point a on KC must lie above the curve OEK. In particular, if DF is the line segment perpendicular to OA which intersects OA at D, OEK at E, KC at a, and OFL at F, then DE < Da by choice of a. This is shown in the figure below (adapted from Gregory's proof-see the Appendix ).
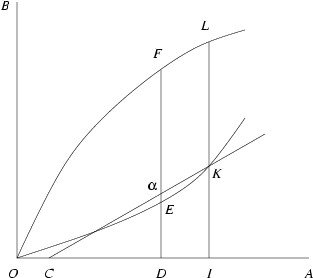
Actually, the figure tells only half of the story. It's also possible that a could lie on the other side of K on the line CK. However, the argument for that case is similar, and the details make a good exercise (or see the Appendix ).
By the definition of the curve OEK, if area(OFD) denotes the area enclosed by the curve OF and the line segments OD and DF, then DE = area(OFD). Likewise, IK = area(OFLI). Thus, IK/DE = area(OFLI)/area(OFD). Since DE < Da, it follows that IK/Da < IK/DE and so
|
|
This last step may seem mysterious, but it serves the purpose of converting the original inequality into an inequality about areas which will lead Gregory to an obvious geometrical contradiction. Specifically, DC·IL is the area of the rectangle with sides IL and DC, and IL·IC is the area of the rectangle with sides IL and IC. Inverting the ratios in the last inequality yields:
|
|
But recall the defining equality for C-namely, IK/IC = IL. This implies that IK = IC·IL. Since IK = area(OFLI) by definition of the curve OEK, the denominators in the last inequality are the same. Therefore, the numerators must satisfy DI·IL < area(DFLI). But remember that OFL is increasing by assumption. Thus, the rectangle with sides IL and DI must circumscribe the region DFLI.
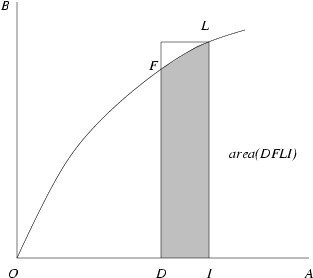
Hence area(DFLI) < DI ·IL as well. This contradiction shows that KC must in fact be tangent to OEK. Hence the fundamental theorem of calculus follows.
Andrew Leahy (Knox College), "A Euclidean Approach to the FTC - Gregory's Proof of the FTC," Convergence (August 2010), DOI:10.4169/loci002156




