- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
An Investigation of Historical Geometric Constructions - Calculating the Area of a Lune II
Since Heath noted that Hippocrates was initially “circumscribing a semicircle about an isosceles right-angled triangle”, it is necessary to begin by constructing an isosceles right-angled triangle as shown in figure 14.

Figure 14: Isosceles right triangle ABC circumscribed by semicircle ABC.
An isosceles-right triangle could also have been constructed using points A, C, and D (see Figure 15). Therefore, AB = BC = CD = DA.
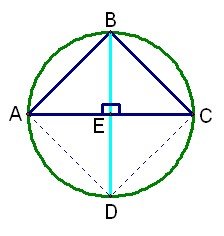
Figure 15: Construction of isosceles right triangle ABC.
Next, we construct a second circle with center D and radius DA to get “a segment of a circle similar to those cut off by the sides” of the isosceles right triangle ABC (see Figure 16). This segment of a circle with base AEC is in a quadrant of a circle and is therefore similar to the two original segments with base AB and BC.

Figure 16: Construction of a circle with center D.
Suzanne Harper and Shannon Driskell, "An Investigation of Historical Geometric Constructions - Calculating the Area of a Lune II," Convergence (August 2010)




