- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Apollonius's Ellipse and Evolute Revisited - The Evolute
The evolute of an ellipse may be defined in terms of the curvature at a point on the ellipse. Suppose that the ellipse is parameterized by [(r)\vec](t)=áacos(t),bsin(t)ñ, 0 £ t < 2p. The curvature k(t) at [(r)\vec](t) can be evaluated using the standard calculus formula in parametric form
|
|
(4) |
If one adopts the definition that the evolute is the locus of the centers of the osculating circles, then for the ellipse it is this parametrized curve C(t) as t varies from 0 to 2p. Since the focal distance from the center along the major axis is c = Ö{a2-b2}, the two cusps of the evolute at a distance c2/a=c(c/a) < c < a along that axis must fall short of the foci inside the ellipse, while the other two cusps exit the ellipse along the minor axis when c2/b > b or a > Ö2 b.
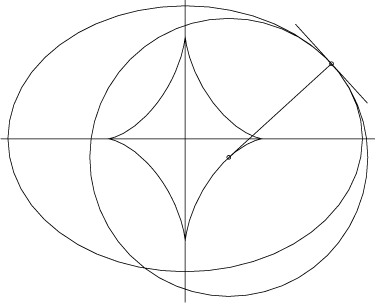
FIGURE 3: The center of the osculating circle traces out the evolute of the ellipse.
Frederick Hartmann and Robert Jantzen, "Apollonius's Ellipse and Evolute Revisited - The Evolute," Convergence (August 2010)




