- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Archimedes' Method for Computing Areas and Volumes - Cylinders, Cones, and Spheres
Recall the following information about cylinders and cones with radius r and height h:
| Solid | Volume | Center of Gravity |
| Cylinder | \(\pi r^2 h\) | On the cylinder's axis, half-way between top and bottom |
| Cone | \(\frac13\pi r^2 h\) | On the cone's axis, three times as far from the vertex as from the base |
Suppose a sphere with radius r is placed inside a cylinder whose height and radius both equal the diameter of the sphere. Also suppose that a cone with the same radius and height also fits inside the cylinder, as shown below.
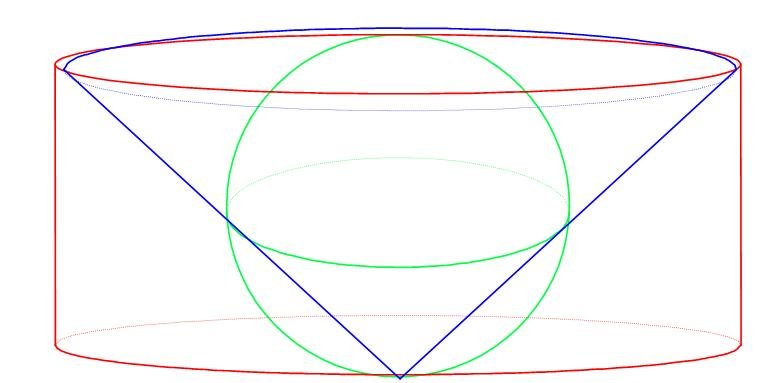
We place the solids on an axis as follows:

For any point S on the diameter AC of the sphere, suppose we look at a cross section of the three solids obtained by slicing the three solids with a plane containing point S and parallel to the base of the cylinder. The cross-sections are all circles with radii SR, SP, and SN, respectively. What Archimedes discovered was that if the cross-sections of the cone and sphere are moved to H (where |HA| = |AC|), then they will exactly balance the cross section of the cylinder, where HC is the line of balance and the fulcrum is placed at A.

This is not hard to show. If the radius of the sphere is \(r\), the origin is at \(A\), and the \(x\) coordinate of \(S\) is \(x\), then the cross-section of the sphere has area \(\pi(r^2-(x-r)^2)=\pi(2r x-x^2)\), the cross-section of the cone has area \(\pi x^2\), and the cross-section of the cylinder has area \(4\pi r^2\). So according to the law of the lever, in order for the above balancing relationship to hold we need to following equation to be true: \[2r\left[\pi x^2+\pi(2r x-x^2)\right]=4\pi r^2 x\] which can easily be verified.
Gabriela R. Sanchis, "Archimedes' Method for Computing Areas and Volumes - Cylinders, Cones, and Spheres," Convergence (June 2016)




