- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Archimedes' Method for Computing Areas and Volumes - The Law of the Lever
Suppose two weights, W and w, are placed on a horizontal weightless stick that rests on a support, called the fulcrum. If W is at a distance D from the fulcrum and w is at a distance d from the fulcrum, then the system will balance if and only if WD=wd.
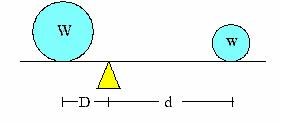
In order to determine the volume of a particular solid, Archimedes would try to find some other solid whose volume he knew, that could be placed in equilibrium with the unknown solid. Then by using the Law of the Lever he could solve for the volume of the unknown solid.
Example:
Suppose we have an orange that we know weighs 4 ounces. By trial and error, we find that when the orange is 2 cm from the fulcrum and a potato is 3 cm from the fulcrum on the opposite side, the system balances. By the Law of the Lever, 4×2 = p×3 (where p is the weight of the potato). Hence p = 8/3 = 2 2/3 oz.
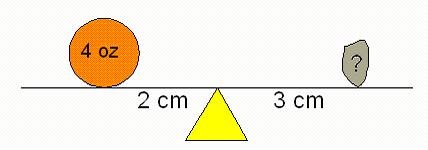
This is precisely the idea that Archimedes used to "discover" the volumes of certain solids. For example, he used his method to find the formula for the volume of a sphere.
Gabriela R. Sanchis, "Archimedes' Method for Computing Areas and Volumes - The Law of the Lever," Convergence (June 2016)




