- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Can You Really Derive Conic Formulae from a Cone? - Why Do Menaechmus' Constructions Work?
Reconsider the mean proportionals x and y of a and 2a: a:x = x:y = y:2a. With the help of modern analytic geometry, we see that this is equivalent to solving simultaneously two of x2 = ay, y2 = 2ax, and xy = 2a2. You should notice immediately that x2 = ay and y2 = 2ax are equations of parabolae, and xy = 2a2 is the equation of a hyperbola. Solving these equations simultaneously is equivalent to intersecting these conics.
Taking the second and third equations and solving them simultaneously gives x3 = 2a3, so a cube of side x has double the volume of a cube of side a.
Was Menaechmus the first to use conic sections? In the same work by Eutocius we have a description of Eratosthenes' (3rd century B.C.) solution to the problem of finding two mean proportionals. In regards to the merits of his own solutions, Eratosthenes is quoted as saying "Do not seek to do the difficult business of the cylinders of Archytas [another method of solution], or to cut the cone in the triads of Menaechmus, or to produce any such curved form in lines as is described by the divine Eudoxus." [14, p. 297]. Based on this quote, it would seem that the "triads of Menaechmus" refers to the three conic sections (we have not yet discussed the ellipse at this point). Because of this Menaechmus is given credit for discovering all three conic sections.
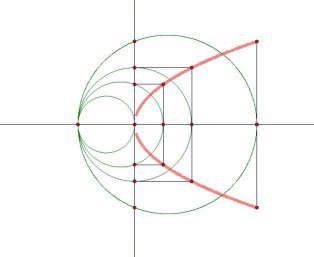
Did Menaechmus actually take sections of a cone? We do not know. The parabola and hyperbola can be constructed pointwise using the geometry of Menaechmus' time. The pointwise generation of the parabola looks something like the graph below.
It is not too hard to imagine the circles in the picture above as horizontal slices of a slanted cone, as shown in the picture [11, p. 117] and GeoGebra animation below.

In the window below, right click and drag to change the viewing angle of the slanted cone and its level curves.
Scholars have taken up this idea and have given probable constructions of conic sections based on sections of a right angled cone [5, pp. 1-4] [9, pp. 111-116]. We take up this discussion in the next sections.
Gary S. Stoudt, "Can You Really Derive Conic Formulae from a Cone? - Why Do Menaechmus' Constructions Work?," Convergence (June 2015)