- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Extending al-Karaji's Work on Sums of Odd Powers of Integers - The Sum of the Cubes
The author of the article on sums of odd powers in Mebahis-i İlmiyye happens to have been the editor of the journal, Vidinli Tevfik Pasha, famous for his algebra textbook (Cecen 1998. For more information about Vidinli Tevfik Pasha, see Sarac 1992.) Vidinli begins his article by quoting the solution of the sum of cubes problem given by al-Karaji in his famous book, al-Fakhri fi'l-jabr wa'l-muqabala, usually known today simply as al-Fakhri. Vidinli refers to al-Karaji’s book as Cebir ve Mukabele (Turkish for al-jabr wa'l-muqabala) and the book is sometimes referred to in English as The Glorious Book of Algebra or The Marvelous Book of Algebra. It was partially translated from Arabic to French by Franz Woepcke in 1853. We were fortunate to find a manuscript copy of al-Fakhri in the Turkish government’s rare book and manuscript library, the Suleymaniye Library.
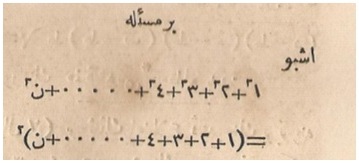
Figure 1 (again). Sum of cubes formula (from Mebahis-i İlmiyye, 1867, courtesy of the authors).
The journal Mebahis-i İlmiyye is written in Turkish using the Arabic alphabet (also known as Ottoman Turkish), and is read from right to left. The Arabic numerals \(0\) through \(9\) appear in Figure 2 (repeated below).

Figure 2 (again). Arabic numerals \( 0\) – \( 9.\)
In Figure 1, the last integer in each sum, at the far left, is the Arabic letter Nun or N and, in Vidinli’s article, is to be understood as we understand “\(n\)”. Regarding his choice of this letter, Vidinli says nothing about what actually appears in al-Karaji’s manuscript or in later surviving copies of it. In particular, he does not report that al-Karaji used the numerical value 10, as can be seen in al-Karaji's manuscript and in Woepcke's translation of it. (See also Beery 2009 and O'Connor and Robertson 1999.) Vidinli does attribute the following geometric justification of the formula \[ 1^3 + 2^3 + 3^3 + \cdots + n^3 = {{(1+2+3+\cdots +n)}^2}\] very clearly to al-Karaji.
Al-Karaji’s geometric justification of his sum of cubes formula begins with a square of side length \( 1 + 2 + 3 + 4\), as shown in Figure 3.

Figure 3. Al-Karaji’s geometric justification of his sum of cubes formula begins with a square of side length \( 1 + 2 + 3 + 4\) (from Mebahis-i İlmiyye, 1867, courtesy of the authors).
Reading from right to left in the first row of equations in Figure 3, Vidinli generalizes the number of line segments making up the lower edge of the square from 4 segments to \(n\) segments by assigning the segments lengths \(1,2,\dots,n.\) Similarly, in the second row of equations, he assigns lengths \(1,2,\dots,n\) to the line segments making up the left edge of the square. (The symbols at the far left of these two rows of equations mean "it continues like this.") The reader can then surmise that the side length of the large square region is \( 1 + 2 + \cdots + n\) and its area is \( {{(1 + 2 + \cdots + n)}^2}.\)
Vidinli then calculates the area of the square region in Figure 3 by adding together the areas of gnomon-shaped regions making up the square, the largest of which is shown in Figure 4a.

Figure 4a. Vidinli first calculates the area of this largest gnomon from the square in Figure 3. (from Mebahis-i İlmiyye, 1867, courtesy of the authors).
Vidinli first calculates the area of the gnomon-shaped region shown in Figure 4a. In Figure 4b, he indicates areas of rectangular regions by juxtaposing the letters at opposite corners of these regions. Reading the first row of equations in Figure 4b from right to left, he has: The sum of the areas of three rectangular regions making up the gnomon is equal to the cube of the length of the line segment at far left in Figure 4a, or \( {n^3}.\) (The overbar plays the role of parentheses.) In the second row in Figure 4b, this area is written as \[ {{(1 + 2 + 3 + \cdots + (n-1))}\times 2n + n^2 = n^3},\] a conclusion that would seem to rely on al-Karaji's knowledge that \[ {{1 + 2 + 3 + \cdots + (n-1)} = \frac{(n-1)n}{2}}.\] (See Exercise 1.)
 Figure 4b. Al-Karaji’s geometric justification of his sum of cubes formula continues with calculation of the areas of gnomons making up the large square (from Mebahis-i İlmiyye, 1867, courtesy of the authors).
Figure 4b. Al-Karaji’s geometric justification of his sum of cubes formula continues with calculation of the areas of gnomons making up the large square (from Mebahis-i İlmiyye, 1867, courtesy of the authors).
In the remaining rows in Figure 4b, Vidinli then calculates the areas of all of the gnomon-shaped regions making up the large square (see Figure 3), indicating the area of each gnomon using the six letters marking its vertices and obtaining areas \[\dots = 2^3,\] \[\dots = 3^3,\] \(\phantom{.}\) \[{\dots \dots \dots,}\] \[\dots = n^3.\]
If we add these areas to the area of the unit square in the lower left corner of the large square, we obtain the sum \[ {1^3 + 2^3 + 3^3 + \cdots + n^3},\] which is equal to the area of the large square of side length \( {1 + 2 + 3 + \cdots + n},\) or to \[ {{(1+2+3+\cdots +n)}^2}.\]
Again, Vidinli clearly attributes this geometric justification to al-Karaji, and indeed al-Karaji's method was to compute the area of each gnomon as that of a square and two rectangles. One wonders exactly how al-Karaji saw that the area of the gnomon in Figure 4a was equal to the cube of the length of the leftmost side of that gnomon. The two journal pages on which Vidinli presents most of al-Karaji’s argument appear in Figure 5.

Figure 5. Al-Karaji’s geometric justification, as presented by Vidinli (from Mebahis-i İlmiyye, 1867, courtesy of the authors).
Hakan Kursat Oral (Yildiz Technical University) and Hasan Unal (Yildiz Technical University), "Extending al-Karaji's Work on Sums of Odd Powers of Integers - The Sum of the Cubes," Convergence (August 2011), DOI:10.4169/loci003725




