- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
External Influences on U.S. Undergraduate Mathematics Curricula: 1950-2000
Abstract
Many of the most important curricular changes in undergraduate mathematics in the second half of the 20th century appear to have been influenced by matters outside mathematics. In many cases these were circumstances in other academic disciplines, but a variety of other external circumstances have been involved as well. We survey a selection of important changes and the external forces that contributed to these changes. There is much more to the history of undergraduate mathematics during 1950-2000 we do not address, but the axis onto which we are projecting is an important one, and not unrelated to current events.
Introduction
In the era from 1950 to 2000 undergraduate teaching of mathematics in the United States was often responsive to external circumstances. This is an interesting phenomenon for a discipline that sometimes claims it has often benefitted the outside world most by following its own internal logic and aesthetics. As will be seen below, the proposals and changes in curricula that demonstrate this recent openness to the external environment are among the most important curricular changes that have occurred during the 1950-2000 era.
This paper is nowhere near a complete history of undergraduate mathematics teaching in the era under consideration – rather, it is a projection onto one important axis. For one thing, we do not consider internal influences impinging on the individual curricular issues considered. (Not, of course, because they were insignificant. We make no claims about their significance relative to the external influences.) Furthermore, we concentrate on impersonal forces, saying only a little about the talented and hard-working leaders who guided our community through these eventful years. Finally, by focusing entirely on curriculum, we ignore many other factors that have shaped our community, our activities and our students: faculty demographics and working conditions; the role of the Advanced Placement program for high school students (as described by David Bressoud’s numerous columns on calculus and the Advanced Placement program in 2010 at [6]); the role of organizations such as the Mathematical Association of America (MAA); the role of journals serving the community; activities related to employment and development of young faculty (the employment register, Project NExT); and so on.
A final disclaimer concerns bias and memory. Having lived through much of this era, we started with a tendency to think that we already understood what happened and why and whether it was a good thing. However, by putting our preferences aside and subjecting our opinions to evidence, we have often surprised ourselves. We hope our work will, likewise, lead some readers to a deeper understanding of our profession. Of course, in historical research, one can never declare that all the evidence is in and, in this spirit, we invite correspondence from readers.
Context
Our work is only a part of what could be a wider investigation in the history of mathematics. It should be supplemented by a similar investigation of teaching in the first half of the 20th century. Would such investigation suggest that high sensitivity to the environment surrounding mathematics instruction in colleges is a timeless feature of American mathematics, or were the years from 1950 to 2000 unusual? Another aspect of the wider problem would compare the impulses expressed in college teaching to those expressed in research. It has been argued by Jeremy Gray [18], that mathematical research underwent a transformation in the decades around 1900 toward modernism, a point of view marked by coolness toward applications and toward the world outside mathematics generally. Gray’s investigation did not reach into the second half of the 20th century. When the multiple strands of research in that second half-century are examined, what balance between modernist and countermodern impulses will we find? And will it appear that there is some linkage between teaching and research in these matters?
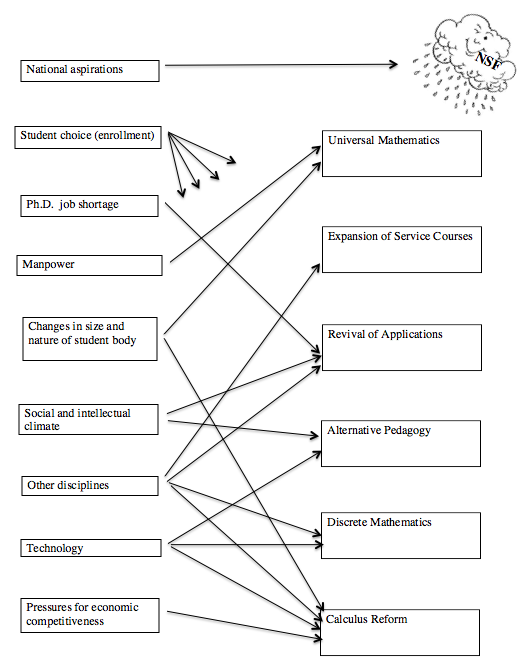
Figure 1. Schematic overview of the present article, "External Influences on U.S. Undergraduate Mathematics Curricula: 1950-2000." External influences are shown at left and new components and characteristics of the undergraduate mathematics curriculum at right.
Overview
Figure 1 is a schematic view of this paper. Our judgment is that all but one of the curricular thrusts in the right hand side of Figure 1 were of considerable importance in what went on in classrooms by the end of the 20th century. The exception is Universal Mathematics, a proposal that was unsuccessful, despite having been devised or supported by some of the most accomplished leaders of our community at the time. We include it because of its eminent pedigree and because it reveals dynamics of the community at that time and how these dynamics differed from more recent ones because of external influences.
The many short arrows leading from Student choice (enrollment) in Figure 1 call for comment. It seems axiomatic that anytime one tries to improve a curriculum one hopes it will draw in more students. But it is surprisingly rare to find explicit comments about this motivation in print – thus the arrows are short and a bit vague about their destinations.
 |
|
Florian Cajori (1859-1930) was a mathematics historian and educator who surveyed undergraduate mathematics curricula in the U.S. for his 1890 book, The teaching and history of mathematics in the United States. The Cajori Two Project, led by the author of this article, has carried his work into the 20th century. Cajori also served as president of the MAA during 1917. (Photo source: Convergence Portrait Gallery) |
There are some curricular changes that do not appear on the right of Figure 1 because they do not seem to have been propelled by external influences to any significant degree. For example, we do not discuss the modernization of the curriculum through the introduction of Modern Algebra, Linear Algebra, and more abstract and rigorous analysis. There are schools where this started before 1950, as we can see from the Cajori Two Project, a survey of undergraduate mathematics courses in the U.S. in the 20th century [40], but most of the change took place in the 1950s and 1960s. This far-reaching change seems to us to have been motivated largely from mathematical research and by the desire to better prepare students for graduate studies in mathematics. Research in modern and linear algebra and modern forms of analysis had been flourishing in the late 19th and early 20th centuries and the gap between undergraduate and graduate studies in these areas had widened.
Impersonal forces propelling proposals for change are sometimes broad, encouraging the general process of change, and sometimes particular, encouraging just one or a few proposals for change. Foundation money, especially from the National Science Foundation (NSF), was undoubtedly a broad force for change [47], symbolized by the friendly cloud in Figure 1. The NSF was founded in 1950 with a very broadly stated mission: "To promote the progress of science; to advance the national health, prosperity, and welfare; and to secure the national defense" [46]. Its budget for Education and Human Resources, of which support for curricular innovation is a part, rose from $0 in fiscal year 1951 to $727.6 million in 2000.
This growth in federal funding for science, mathematics and engineering had a large effect on mathematics education. As an example, starting in 1976, it became possible for a non-profit mathematics curriculum development organization, the Undergraduate Mathematics Applications Project (UMAP) and, later in 1980, its successor the Consortium for Mathematics and its Applications Project (COMAP), under the direction of Solomon (Sol) Garfunkel, to sustain itself in large part through its work on NSF grants. COMAP’s activities would eventually involve a wide variety of undergraduate mathematics courses, especially the popular lower division courses. COMAP had an especially large impact on re-introducing applications to the curriculum.
For another glimpse of how the growth of external funding has altered our professional world, we turn to a brief description of an early proposal for change so that we may examine how starkly it differed from a modern curricular thrust such as calculus reform.
Walter Meyer (Adelphi University), "External Influences on U.S. Undergraduate Mathematics Curricula: 1950-2000," Convergence (August 2013)




