- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Francois-Joseph Servois: Priest, Artillery Officer, and Professor of Mathematics - Early Publications
While at Metz, Servois began publishing and presenting his mathematical research. His first paper, written in 1805, was a treatise on expanding functions into power series. This paper was presented to the Institut National des Sciences et des Arts* and would undergo several revisions to become his celebrated “Essay” [Servois 1814a] on the foundations of the differential calculus. (The next section describes this paper in more detail.)
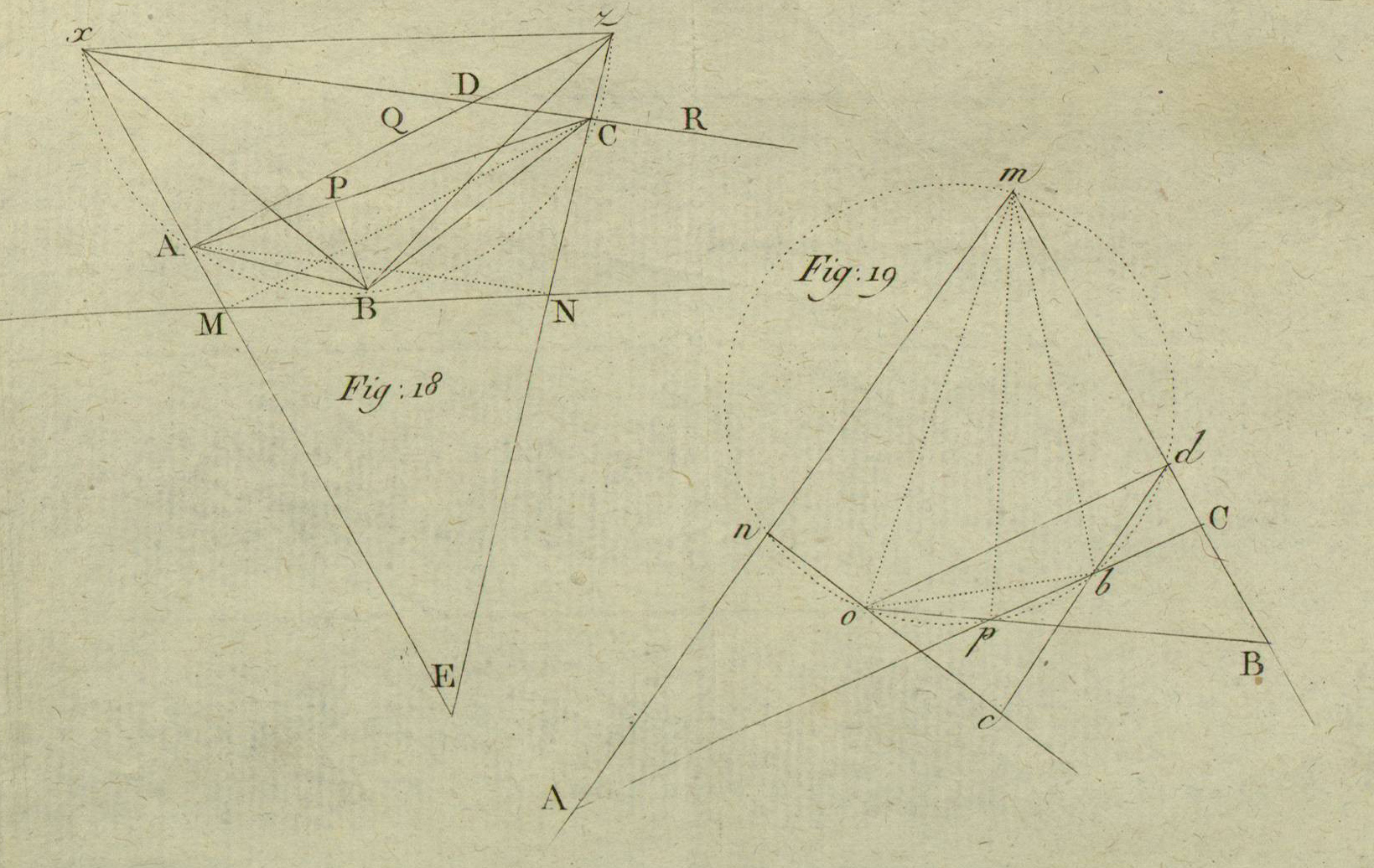
Figure 3. Figures from Servois' geometry text (public domain). The left-hand figure was used to construct a parallel to an inaccessible line. The right-hand figure was used to prolong a line beyond an obstacle. The dotted circles in these figures are not part of the constructions, but rather used to verify the validity of the constructions.
Additionally, Servois published his first and only book, titled Solutions peu connues de différents problèmes de géométrie-pratique [Servois 1804] (Little-known Solutions to Various Problems in Practical Geometry) in 1804.** Servois' geometry text was intended to be a reference on applied geometry for military officers, presenting constructions in ruler-geometry that could be used on the battlefield at any time [Bradley 2002]. Taton [1972] stated that the work was well received by the public and Jean-Victor Poncelet (1788-1867) declared Servois' book to be
a truly original work, notable for presenting the first applications of theory of transversals to the geometry of the ruler or surveyor's staff, thus revealing the fruitfulness and utility of this theory [Poncelet 1865, p. 44].
The geometry textbook is divided into two sections after a brief introduction: Theory and Practice. There is an index of the practical section, errata, and a table of figures. It is also bound with a 28-page article, a “Letter from S … to F …, Professor of Mathematics” who is possibly François Joseph Français (1768-1810). The military applications of the geometry text can be seen in the following index of the practical section. Note that all of these constructions are performed with straightedge, but no compass.
- To prolong a line beyond an obstacle.
- To find a point aligned with the two invisible points of intersection of two pairs of lines given in direction.
- From a given point, to draw a line to the invisible point of intersection of two lines given in direction.
- At a given point, to draw a line parallel to two other parallels given in direction.
- To draw two parallel lines on the ground.
- From a given point, to draw a parallel to an accessible line.
- From a given point, to draw a parallel to an inaccessible line.
- To divide a line into two equal parts.
- To divide a line into any number of equal parts.
- To divide an accessible angle into two equal parts.
- To divide an inaccessible angle into two equal parts.
- To erect a perpendicular on a line at a given point.
- From an inaccessible point, to drop a perpendicular to an accessible line.
- From a given point, to drop a perpendicular to an inaccessible line.
- To measure a line, one of whose extremities is inaccessible.
- To measure an inaccessible line.
- To measure the distance from a point to an inaccessible line.
Interestingly, Poncelet consulted Servois for his expertise on geometry several times during the writing of the 1822 edition of the Traité des propriétés projectives [Taton 1972].
Servois was eventually transferred to the artillery school at La Fère, where he presented papers on the elements of dynamics and on cometary and planetary orbits to the Institut. However, these papers were never published [Taton 1972]. Then in 1810, he wrote and published his “De principio velocitatum virtualium commentatio,” a paper elaborating Joseph-Louis Lagrange's (1736-1813) notion of “virtual velocities.” The paper was entered in a prize competition sponsored by the Academy of Turin. Curiously, his memoir was the only entry the Academy received and, because Servois missed the deadline, nobody won the prize. However, the paper was deemed worthy, so the Academy published it and elected him a corresponding member [Bradley 2002].
________________________
*After the French Revolution, the Royal Academy of Sciences of Paris, along with other royal societies, were incorporated into the Institut National des Sciences et des Arts, renamed the Institut de France in 1806.
**The year of publication is given as 1805 in [Poncelet 1865, Taton 1972], but is actually year XII of the French Revolutionary calendar, which translates to 1804 or late 1803.
Salvatore J. Petrilli, Jr. (Adelphi University), "Francois-Joseph Servois: Priest, Artillery Officer, and Professor of Mathematics - Early Publications," Convergence (November 2010), DOI:10.4169/loci003498




