- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Historical Activities for Calculus - Module 3: Optimization – Galileo and the Brachistochrone Problem
Galileo and the Brachistochrone Problem
The last optimization problem that we discuss here is one of the most famous problems in the history of mathematics and was posed by the Swiss mathematician Johann Bernoulli in 1696 as a challenge “to the most acute mathematicians of the entire world.” The problem can be stated as follows:
Given two points on a plane at different heights, what is the shape of the wire down which a bead will slide (without friction) under the influence of gravity so as to pass from the upper point to the lower point in the shortest amount of time?

Figure 46. Brachistochrone Problem: Which path from \(A\) to \(B\) is traversed in the shortest time? (Click image to animate.)
This is the Brachistochrone (“Shortest Time”) Problem. This was a different kind of optimization problem, since instead of asking for the value of a variable, among all possible values, that would maximize or minimize something, it asked for the optimal function (or curve), among all possible curves. The differential calculus does not provide all the tools necessary to solve this problem. So for the moment, we would like to discuss Galileo Galilei's work relevant to this problem, which occurred in 1638, well before the Brachistochrone Problem had been explicitly stated.
Galileo studied motion under gravity, showing that a body falling in space traverses a distance proportional to the square of the time of descent. Using this law, he was able to compute the time of descent of an object falling along an inclined plane from point \(A\) to point \(B,\) assuming no friction.
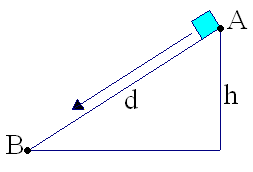
Figure 47. Galileo's formula for time of descent along an inclined plane, as shown in the diagram:
The time to travel from \(A\) to \(B\) is \[\sqrt{\frac{2}{g}}\cdot\frac{d}{\sqrt{h}}\] where \(d\) is the distance between points \(A\) and \(B\) (in meters), \(h\) is the vertical distance between \(A\) and \(B\) (in meters), and \(g\) is the acceleration due to gravity, approximately \(9.80\) \(\mbox{m}/\mbox{sec}^2.\)
Clearly the shortest path from \(A\) to \(B\) is a straight line, but is this path the one that will take the shortest time? For example, is there some point \(C\) such that if the body were to fall following a straight line from \(A\) to \(C,\) and then a straight line from \(C\) to \(B,\) as shown in Figure 48, it would do so in less time than if it traversed a straight-line path from \(A\) to \(B?\)
Figure 48. Does the body fall from point \(A\) to point \(B\) in less time along the path \(A\rightarrow B\) or along the path \(A\rightarrow C\rightarrow B?\)
Galileo appeared to believe that the answer to the brachistochrone problem was an arc of a circle; that is, that the path \(A\rightarrow C\rightarrow B\) in Figure 48 should be replaced by a circle passing through points \(A\) and \(B.\) Was Galileo correct?
Figure 49. Use this GeoGebra applet to explore the Brachistochrone Problem by comparing the times of descent along different polygonal paths.
Exercises
Exercise 13.
Use a CAS to define the following two functions:
\[T(a,b,c,d,u):=\frac{\sqrt{(a-c)^2 + (b-d)^2}\cdot\left(\sqrt{2g(b-d) + u^2}-u\right)}{g(b - d)}\]
\[V(a, b, c, d, u):=\sqrt{2g(b-d) + u^2}\]
where \(g\) has been predefined to be 9.8 (the acceleration due to gravity in meters per square seconds). The function \(T(a,b,c,d,u)\) computes the time of descent from \(A(a,b)\) to \(B(c,d)\) along a straight-line path, assuming no friction and initial velocity \(u.\) The function \(V(a,b,c,d,u)\) gives the terminal velocity. We assume distance is measured in meters and time in seconds.
(a) Compute \(T(0,0,5,-5,0)\) to find the time of descent from \(A(0,0)\) to \(B(5,-5)\) along an inclined plane, assuming no friction and an initial velocity of \(0.\)
(b) To compute the time of descent along the polygonal path \((0,0)\) to \((1,-2)\) to \((5,-5),\) you need to add the time it takes along \((0,0)\) to \((1,-2),\) which is \(T(0,0,1,-2,0),\) and the time it takes along \((1,-2)\) to \((5,-5),\) which is \(T(1,-2,5,-5,v_1)\) where \(v_1\) is the terminal velocity from the first part of the path, i.e. \(v_1=V(0,0,1,-2,0).\) Hence compute \[T(0,0,1,-2,0)+T(1,-2,5,-5,V(0,0,1,-2,0)).\]
(c) Suppose we want a polygonal path \((0,0)\) to \((x,y)\) to \((5,-5)\) where \((x,y)\) lies on the circle \((x-5)^2+y^2=25.\) Solving for \(y,\) where \(-5\leq y\leq 0,\) we obtain \(y=-\sqrt{25-(x-5)^2},\) so our point \((x,y)\) must be of the form \(\left(x,-\sqrt{25-(x-5)^2}\right)\) in order to lie on the quarter circle. The time of descent for this path then is
\[T\left(0,0,x,-\sqrt{25-(x-5)^2},0\right)+T\left(x,-\sqrt{25-(x-5)^2},5,-5,V\left(0,0,x,-\sqrt{25-(x-5)^2},0\right)\right)\]
Use a CAS and calculus to find the value of \(x\in(0,5)\) that minimizes the above quantity. Compare the time of descent along this polygonal path to the time along the straight line path.
(d) Let \(C\) be the point whose \(x\)-coordinate you found in part 3. Galileo knew that any polygonal path \((0,0)\) to \(C\) to \((5,-5),\) where \(C\) is on the circle, would take less time than the straight line path \((0,0)\) to \((5,-5).\) He then reasoned that if you added another point \(D\) on the circle to form the path \((0,0)\) to \(C\) to \(D\) to \((5,-5),\) the time of descent for this path would be less than the time for the path \((0,0)\) to \(C\) to \((5,-5).\) Find \(D=\left(x,-\sqrt{25-(x-5)^2}\right),\) so that the time of descent for the polygonal path \((0,0)\) to \(C\) to \(D\) to \((5,-5)\) is smallest. What is the total time for the path \((0,0)\) to \(C\) to \(D\) to \((5,-5)?\)
Exercise 14.
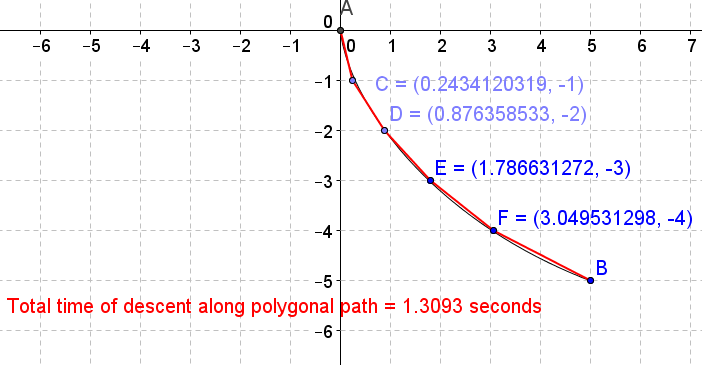
(a) Use calculus to find the value of \(x\) so that the time of descent along \((0,0)\) to \((x,-1)\) to \((5,-5)\) is the smallest. Let \(C=(x_1,-1)\) be the point that minimizes the time of descent. Also compute the terminal velocity \(v_1\) on the path \((0,0)\) to \(C.\)
(b) Use calculus to find the value of \(x\) so that the time of descent along \(C\) to \((x,-2)\) to \((5,-5)\) is the smallest, where the initial velocity at \(C\) is \(v_1.\) Let \(D=(x_2,-2)\) be the point that minimizes the time of descent. Also compute the terminal velocity \(v_2\) on the path \(C\) to \(D.\)
(c) Use calculus to find the value of \(x\) that minimizes the time of descent along \(D\) to \((x,-3)\) to \((5,-5)\), where the initial velocity at \(D\) is \(v_2.\) Let \(E=(x_3,-3)\) be the point that minimizes the time of descent. Also compute the terminal velocity \(v_3\) on the path \(D\) to \(E.\)
(d) Finally, use calculus to find the value of \(x\) that minimizes the time of descent along \(E\) to \((x,-4)\) to \((5,-5),\) where the initial velocity at \(E\) is \(v_3.\) Let \(F=(x_4,-4)\) be the point that minimizes the time of descent. Also compute the terminal velocity \(v_4\) on the path \(E\rightarrow F.\)
Figure 50. Diagram for Exercise 14, part e
(e) Compute the time of descent along the the path from \(A(0,0)\) to \(C\) to \(D\) to \(E\) to \(F\) to \(B(5,-5).\) How does this compare to the time of descent along the polygonal path \((0,0)\) to \(C\) to \(D\) to \((5,-5)\) that you computed in the previous exercise?
Figure 51. Applet for Exercise 14, part f
(f) The applet in Figure 51 contains the construction of an (upside-down) cycloid, a curve traced out by a point on the circumference of a circle as it rolls along a straight line. Drag \(C\) to rotate the circle. The curve goes through \(A(0,0),\) but it doesn't go through \(B(5,-5).\) You can find a cycloid that goes through \(B\) by adjusting the radius \(r\) of the rolling circle. What is the radius of the generating circle that produces a cycloid that goes through both \(A\) and \(B?\)
It turns out that this cycloid is the answer to the Brachistochrone Problem for any points \(A\) and \(B,\) not just \(A=(0,0)\) and \(B=(5,-5).\) Add the points on the polygonal path that you found above to the list of points in the applet. Your cycloid should be a pretty good fit.
Gabriela R. Sanchis (Elizabethtown College), "Historical Activities for Calculus - Module 3: Optimization – Galileo and the Brachistochrone Problem," Convergence (July 2014)