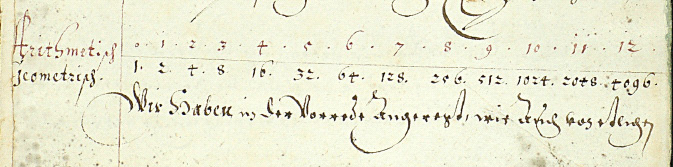- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Logarithms: The Early History of a Familiar Function - Joost Bürgi Introduces Logarithms
At about the same time in Switzerland, Joost Bürgi, a court clock maker by profession, grappled with the same issues of computation. Bürgi's key motivation was not only to facilitate computation, but also to produce a single table that could be applied to all arithmetical operations, rather than needing various tables to perform them all. In his work, Arithmetische und Geometrische Progress Tabulen (Arithmetic and Geometric Progression Tables), published in 1620, Bürgi noted that having separate tables for multiplication, division, square roots, and cube roots is “not alone irksome, but also laborious and cumbersome” (Preface, 1, xi-xii).

Figure 5. Joost Bürgi (1552-1632)
(from MacTutor History of Mathematics Archive)
Furthermore, Bürgi grounded his conception directly in the relation between two progressions. He stated that he was able to create one table for a multiplicity of calculations by considering two “self-producing and corresponding progressions” (Preface, 1, xv-xvi): one arithmetic and the other geometric. To illustrate the underlying principle by means of “nice” numbers, he gave corresponding progressions based on the powers of two, as shown in Figure 6.
Figure 6. Bürgi presents an arithmetic progression (top numbers in red) \(0,1,2,3,\) ... and beneath it a corresponding geometric sequence, \(1,2,4,8,\) ...; that is \(2^0,2^1,2^2,2^3\),...
(Image used by permission of University Library - Graz)
Bürgi gave the relation of powers of two as an example, but in fact different parameters underpinned his logarithmic relation. As he noted, successive powers of two increase too quickly to be useful to interpolate between values so instead he used a common ratio of \(1.0001\), and the successive values were tabulated as follows: \[b_{n+1} = b_{n}(1.0001)\;\;{\rm where}\;\;b_{0} = 10^8\]
Thus, each successive value in the table can be generated by multiplying the previous one by \(1.0001\). Bürgi used the factor of \(10^8\) to allow for greater integer precision.
For example, the logarithm of \(101907877\) (a black number) can be found using the tables as follows (we must note that his logarithm values increased by \(10\) and were also multiplied by a factor of \(10\)).
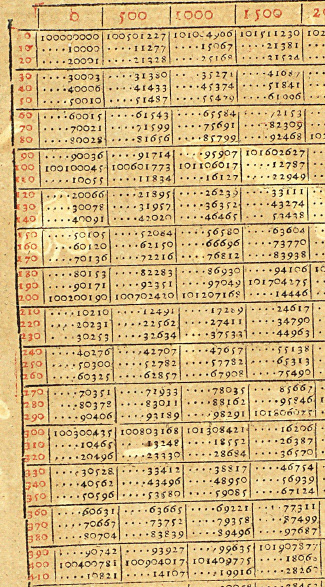
Figure 7. Locating a logarithm value
(Image used by permission of University Library - Graz)
One takes the black number \(101907877\) from the table (see Figure 7) and finds the corresponding red number or logarithm; in this case it is \(189\). To check the value \(101907877\), we see: \[101907877 = (10^8)(1.0001)^{189}.\]
One of the interesting aspects of Bürgi's system was his use of color to emphasize the relationship between the arithmetic and geometric progressions. Unlike Napier, Bürgi did not develop technical terminology to capture the relationship, but simply referred to numbers and their logarithmic counterparts as black numbers and red numbers, respectively, and used black and red ink to maintain this distinction. This was done consistently throughout the text as well as in the tables: the arguments of tabulation, the logarithms, are printed in red, and the tabular entries, the ordinary numbers or antilogarithms, are printed in black.
Bürgi stated that his tables could be used for all manner of calculations, including multiplication, division, extraction of roots, and computing mean proportionals. He provided some 26 examples of the various calculations and the corresponding use of the tables. Here we examine two of his examples. To multiply two numbers using the tables, Bürgi simply listed the black numbers (antilogarithms), identified their corresponding red numbers (logarithms) and added them, and finally determined the black number corresponding to the sum. (Bürgi described linear interpolation methods whenever corresponding black or red numbers were not found in the tables.) For example, Bürgi set out \(154030185\) to be multiplied by \(205518112\) (given as black numbers). To do this he found their corresponding logarithms (red numbers) in the tables, then added them together, then converted the resulting red number back to its original (antilogarithmic) black number, as follows:
| \(154030185\times 205518112\) | \(\leftrightarrow\) | \(\log_{burgi}(154030185)\)+\(\log_{burgi}(205518112)\) |
| =\(43200\)+\(72040\) | ||
| =\(115240\) |
This sum, \(115240\), is then located in the tables and the corresponding black number (the product) is \(316559928\).
The cube root of a very large number is also easily computed using Bürgi's tables. For example, to extract the cube root of \(561203700\) (a given black number), Bürgi located the corresponding logarithm (red number) and simply took a third of it, as follows: \[\sqrt[3]{561203700}\Rightarrow \log_{burgi}(561203700) = 172500\]
\[172500 \div 3 = 57500\]
\[57500 = \log_{burgi}(X) \Rightarrow X = 177.707944 \;{\rm as}\;{\rm required}\] so that the desired cube root is \(177.707944\). This process bypasses an involved cube root extraction algorithm.
Bürgi computed logarithms for \(100 000 000\) to \(1 000 000 000\). This filled fifty-eight pages of tables for a total of 23,030 entries (23,027, plus an additional 3 entries) to be computed to eight significant digits. In addition to the tables, Bürgi wrote an accompanying text, which gave his general motivations as well as many worked examples to show exactly how the tables could be used to lessen the labors of computation. These were published in 1620, although there are reasons to suppose that the tables were in existence prior to this time.
Kathleen M. Clark (The Florida State University) and Clemency Montelle (University of Canterbury), "Logarithms: The Early History of a Familiar Function - Joost Bürgi Introduces Logarithms," Convergence (January 2011), DOI:10.4169/loci003495