- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematical Treasure: Copernicus' De Revolutionibus
De revolutionibus orbium coelestium by Nicolas Copernicus first appeared in 1543. Comprised of six books, the treatise argued for acceptance of the heliocentric, or sun-centered, theory of the planetary orbits. Copernicus based his findings on mathematics rather than physics. The edition whose title page is shown below is from 1566.

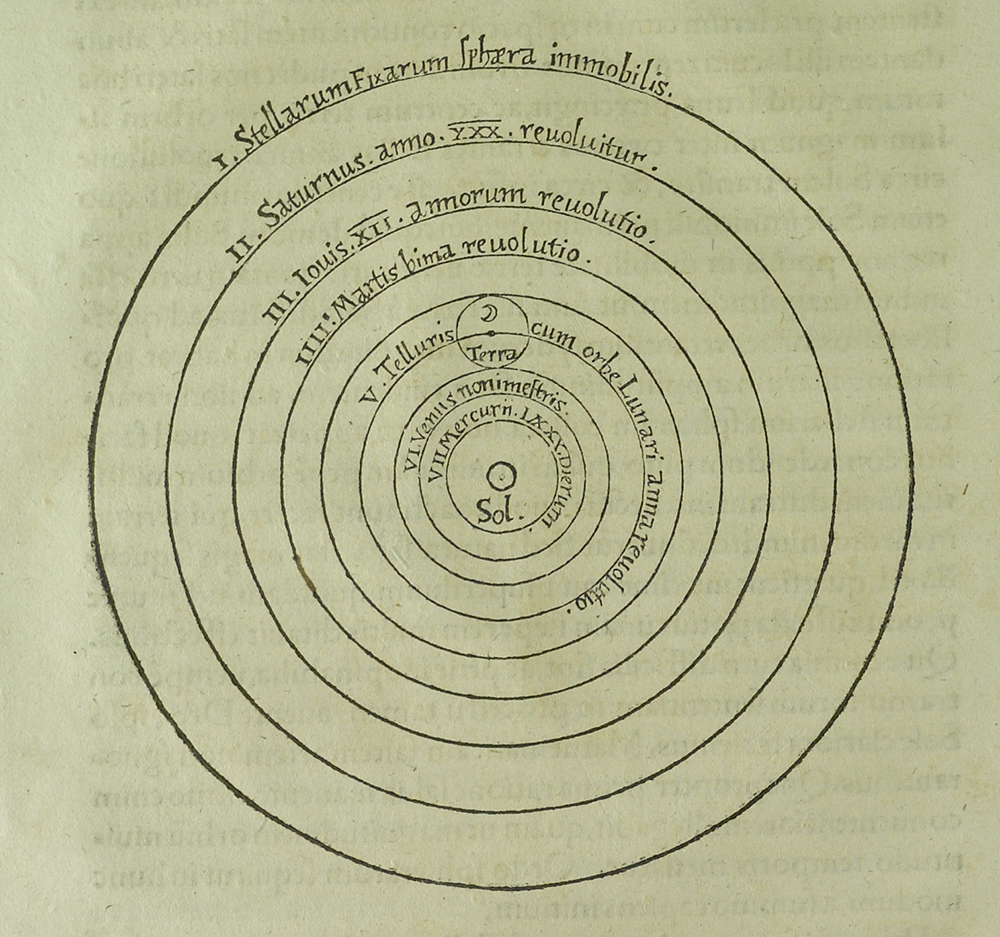
Copernicus’ sun-centered system still employed circular, rather than elliptical, orbits, as shown in the following diagram.

The lefthand page above (page or folio 9v or "9 verso") may be the most famous in the whole book, as its diagram shows clearly the orbits of the planets about the Sun, with the Earth ("Terra") indicated by the circle just above the Sun. This diagram is shown below.
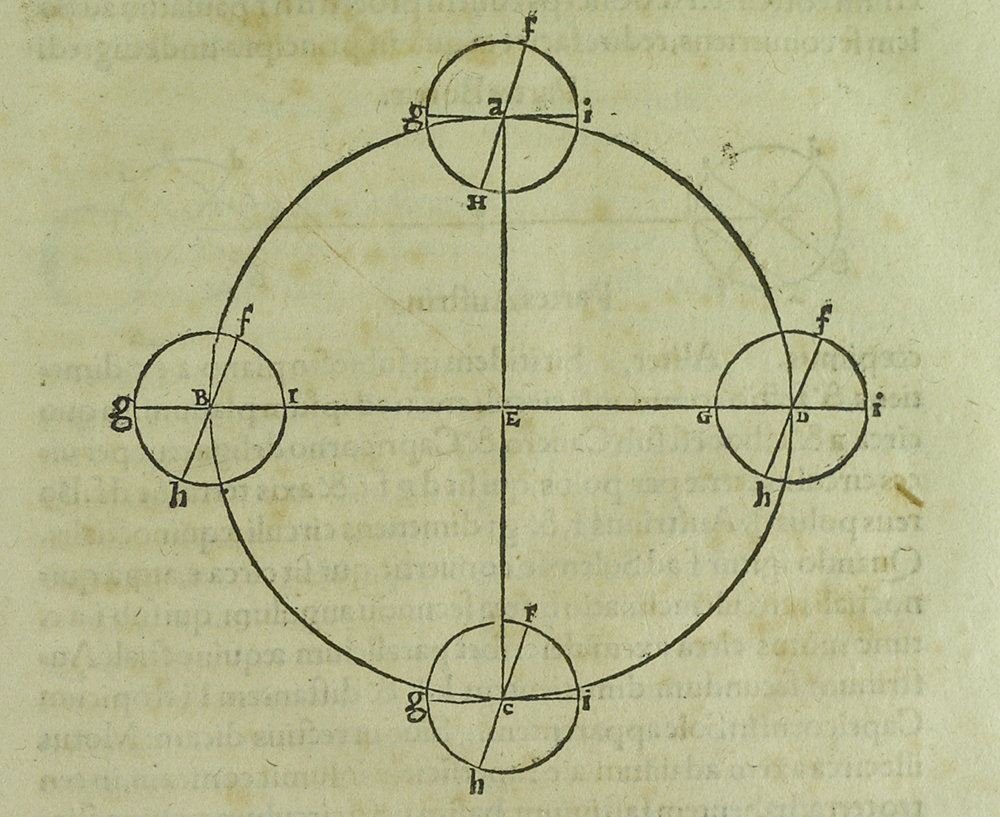
The following diagram is found in Book I, Chapter 11, "Demonstration" or “Proof of the Earth’s triple motion.”

On page 142 of Chapter 4 of Book V, Copernicus asked, “In what ways do the planets’ own motions appear non-uniform?”


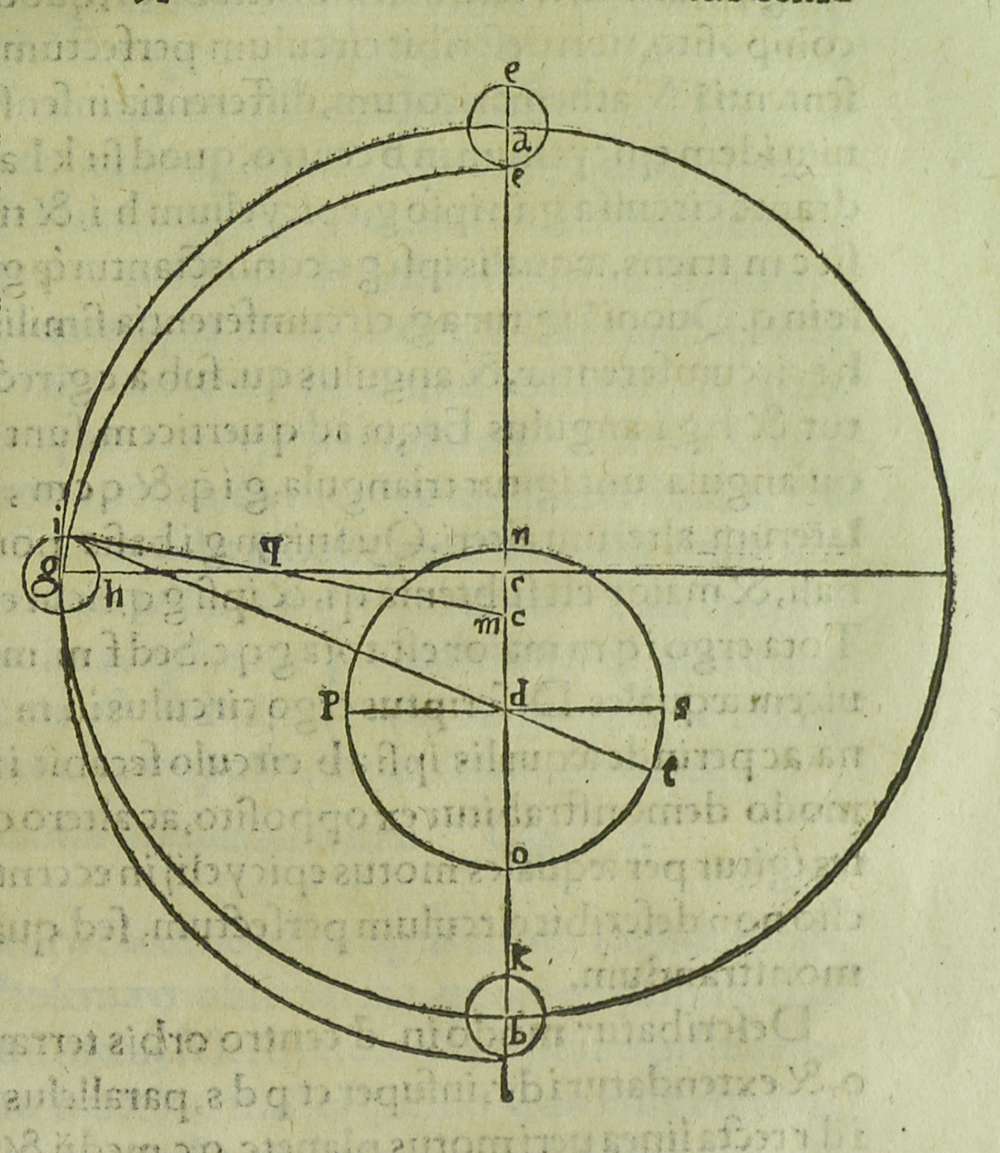
Continuing the discussion begun in Chapter 4, Copernicus focused in Chapter 5 on "Demonstrations" or “Proofs of Saturn’s motion” (see bottom of righthand page 143).

For additional images from De revolutionibus, see the University of Glasgow (Scotland) copy annotated by both Gerardus Mercator and Willebrord Snell. Be sure to follow the link at this page to more images of De revolutionibus in a University of Glasgow “Book of the Month” webpage from April of 2008.
An excellent English language translation of De revolutionibus by Edward Rosen was published in 1978, with a paperback reprint in 1992. Its title is On the Revolutions: Nicholas Copernicus Complete Works, translation and commentary by Edward Rosen, Johns Hopkins University Press.
The Special Collections staff at the Linderman Library of Lehigh University in Bethlehem, Pennsylvania, is pleased to cooperate with the Mathematical Association of America to exhibit this and other items from the Library’s holdings in “Mathematical Treasures.” In particular, Convergence would like to thank Lois Fischer Black, Curator, Special Collections, and Ilhan Citak, Archives and Special Collections Librarian, for their kind assistance in helping to make this display possible. You may use these images in your classroom; all other uses require permission from the Special Collections staff, Linderman Library, Lehigh University.
Frank J. Swetz (The Pennsylvania State University), "Mathematical Treasure: Copernicus' [i]De Revolutionibus[/i]," Convergence (February 2013), DOI:10.4169/loci003956




