- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematical Treasures - Sacrobosco’s Algorismus
This is the opening page of a 1490 manuscript copy of Johannes de Sacro Bosco’s Tractatus de Arte Numerandi, sometimes referred to as his Algorismus, as indicated in the first line of text below. Sacro Bosco or Sacrobosco (circa 1195-1256), as he is best known, was called many other names, including John of Holywood. He was a British monk and a professor at the University of Paris. While particularly well known for his book on astronomy, Tractatus de Sphaera, his Algorismus was also important. The tract went through 12 editions within 33 years and remained influential up to the Renaissance. By writing on the Hindu-Arabic numerals (or Indo-Arabic numerals) and their operations, including root extraction, he affirmed their usefulness and importance. As a result of this effort, the new numerals were accepted and taught at the universities.

Sacrobosco’s opening line on the page above indicates that the art of numbering in history proceeded from the origins of proportion and the quantifying of events. Further, he erroneously attributed the founding of the Hindu-Arabic numeration system to a philosopher Algus or Algor, from whose name the term algorism was derived. This misconception was formed by previous European writers who thought Algor to be a legendary Indian king or philosopher. At the bottom right of this page, Sacrobosco listed the numerals in descending order 0, 9, 8, …, 1 in the manner recorded by Leonardo of Pisa in his 1202 Liber abaci.

The second page of Sacrobosco’s Algorismus explains how to construct higher order numbers as powers of ten. The first statement notes that zero, or cifra, by itself denotes nothing but, when placed to the right of a digit, signifies place value. The pointing hand indicates important information (we might write “N.B.”), in this case, the association of digit string length to number size, up to seven digits denoting millions. Sacrobosco also noted that the process of increasing number size by multiplying by powers of ten could continue up to infinity.
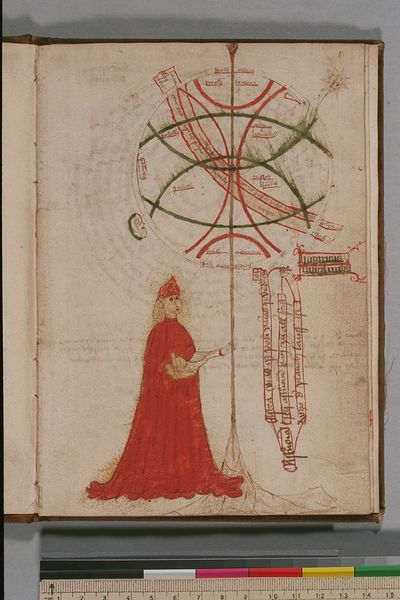
The title page from another fifteenth-century manuscript copy, made in Germany, depicts Astronomy in flowing red robes, holding a representation of the earth divided into zones (the red lines) with the courses of the moon and the sun (the green lines). The scroll contains one line of Latin: it’s the first of an 11-line poem in which each of the seven liberal arts introduces herself, followed by lines for Philosophy, Nature, the Trinity and Wisdom. Astronomy continues here in German: “I, Astronomy, can know above all others what the course the planets run.” The owner, and probably producer, of the book proudly names himself on this page, Hainrich Muglinck, and elsewhere he declares himself the “astronomer of astronomers.”
The first two images above are provided courtesy of the Beinecke Rare Book and Manuscript Library, Yale University. You may use them in your classroom; all other uses require permission from the Beinecke Rare Book and Manuscript Library. The Mathematical Association of America is pleased to cooperate with the Beinecke Library and Yale University to make these images available to a larger audience. The third image shows Plimpton MS 184 at Columbia University. An earlier manuscript may also be viewed in Mathematical Treasures.
Frank J. Swetz (The Pennsylvania State University), "Mathematical Treasures - Sacrobosco’s Algorismus," Convergence (April 2014)




