- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Maya Cycles of Time: Maya Calendrics
Like all Mesoamerican cultures, the Maya employed a 260-day year called the Tzolkin or sacred almanac. Dates consisted of pairings of two cycles, one cycle of 13 day numbers with another of 20 day names.

In this almanac, the day 1 Imix is followed by 2 Ik, 3 Akbal, and so on, passing through 260 unique pairs of day numbers and names illustrated by interlocking wheels.

Figure 3. Tzolkin calendar. David Pratt.
The Maya also used the standard Mesoamerican 365-day Haab, or vague year, composed of eighteen months of 20 days, numbered zero through nineteen, and closing with the 5-day month of Uayeb.

The Haab roughly approximates a solar (or tropical) year and the Maya recorded an accurate account of the discrepancy. Great observers of the cycles of time, they noted that a 365-day year precessed through all the seasons twice in 1,101,600 days (a number that will become significant later). Thus, the true length of a year, \(n,\) satisfies \[\frac{1101600}{365} = \frac{1101600}{n} + 2,\] so that \(n=365.242036\) days, which is slightly more accurate than our Gregorian calendar.
A Calendar Round combined the 260-day Tzolkin and 365-day Haab year in ancient Mesoamerica. As the least common multiple of 260 and 365 is 52 x 365, the Calendar Round was comprised of 52 Haab years. Thus a typical Calendar Round date referenced both the Tzolkin and Haab positions. For example, the date 11 Akbal 16 Ceh would look like
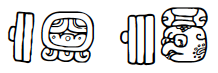
in Mayan glyphs with the number glyphs rotated from horizontal to vertical. The Calendar Round can be illustrated by interlocking wheels as shown in Figure 4, with the two wheels on the left illustrating the Tzolkin calendar and the partially visible wheel on the right the Haab calendar.
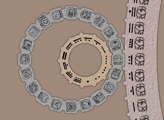
Figure 4. Calendar Round. David Pratt.
Only four of the twenty Tzolkin day names could possibly align with the first position of any month of the 365-day haab year. This is because the sequence of 20 distinct day names and 20-day months align exactly save for the final 5-day month of Uayeb. This misalignment shifts the day name of the start of each successive year by 5. Thus, in any given year, each Haab month begins on the same Tzolkin day. Then in the subsequent year, each month begins 5 days later. In the Classic Era (200–900 CE) these were the days named Akbal, Lamat, Ben, and Etz’nab, and were known as year-bearers. By the time of the Spanish Conquest, the year-bearers had inexplicably been shifted forward by one day. In any case, the four year-bearer day names together with the day numbers 1–13 made up the 52 distinct Tzolkin days beginning each month of a 365-day Haab year of a Calendar Round.
Sandra Monteferrante (Dowling College), "Maya Cycles of Time: Maya Calendrics," Convergence (July 2012), DOI:10.4169/loci003886




