- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Proportionality in Similar Triangles: A Cross-Cultural Comparison - The Student Module
What follows is a sequence of guided student exercises.
(a) Given similar right triangles ABC and DEF below, let b1 be the length of AB, b2 that of DE, h1 that of CB, and h2 that of FE (Figure 6).
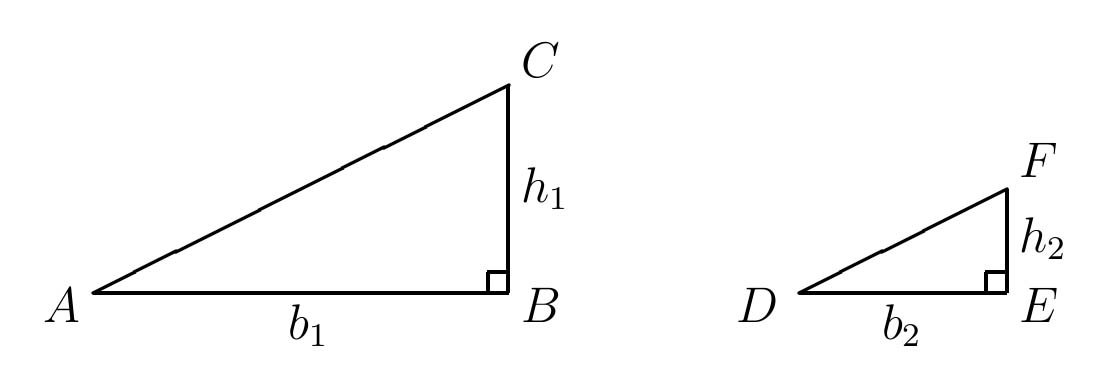
Figure 6: Similar Right Triangles.
By definition of similar triangles, ∠A \(\cong\) ∠D, ∠B \(\cong\) ∠E, ∠C \(\cong\) ∠F. For part (a), consider as given that both ∠B and ∠E are right angles. Prove that
|
by the following outline. Place point D on point C so that the points A, C, and F are collinear (Figure 7).
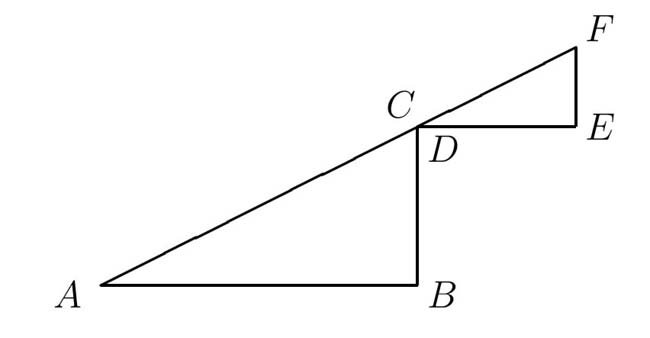
Figure 7: Arrangement of the Triangles.
Duplicate triangle ABC to form triangle AJC, and duplicate triangle DEF to form triangle DLF, pictured below (Figure 8).
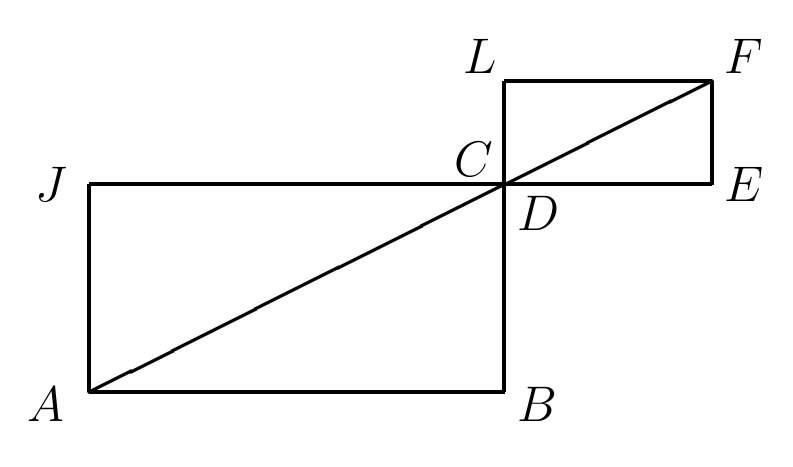
Figure 8: The Duplicated Triangles.
Why are ∠JAB and ∠EFL both right angles? Explain why lines AJ and FL, if extended, will meet in a right angle. Also, explain why lines AB and FE, if extended, will meet in a right angle. Let K and M be these two points of intersection, respectively. Sketch the resulting rectangle AKFM, and apply the inclusion-exclusion principle to find an algebraic expression for the area of the sub-rectangles KLCJ and DEMB in terms of b1, b2, h1, h2. What can be concluded from the resulting equation?
(b) In triangle ABC and triangle DEF (Figure 6) let d1 be the length of AC and d2 the length of DF. Use the gou-gu (Pythagorean) theorem and the result of part (a) to prove algebraically that
|
(c) Develop a version of the inclusion-exclusion principle that applies to an arbitrary parallelogram ABCD (Figure 9).

Figure 9: Parallelogram ABCD .
Begin by constructing diagonal DB and choosing a point H along the diagonal.
(d) Let triangle ABC and triangle DEF be arbitrary similar triangles (not necessarily right triangles) with ∠A \(\cong\) ∠D, ∠B \(\cong\) ∠E, ∠C \(\cong\) ∠F (Figure 10).
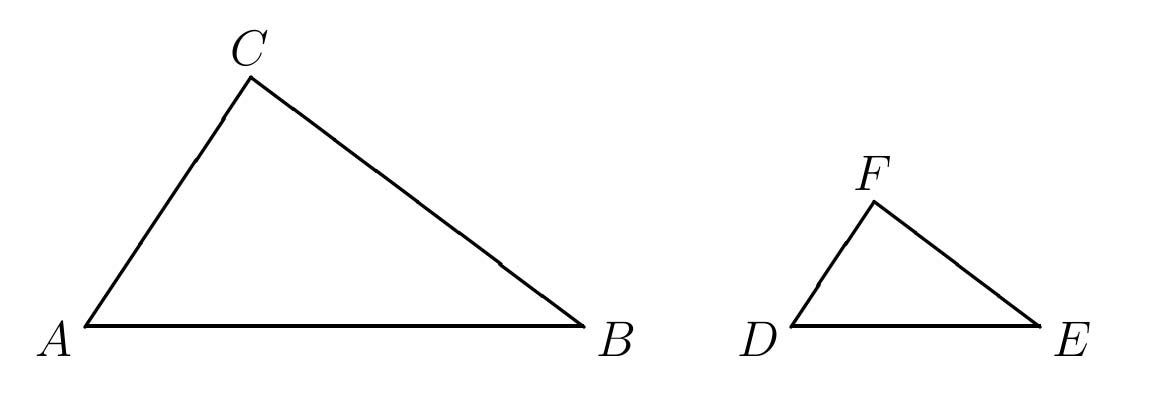
Figure 10: Arbitrary Similar Triangles.
Let b1 be the length of AB, b2 the length of DE, s1 the length of CB, and s2 the length of FE. Prove that
|
using either of the strategies below.
1. Apply the inclusion-exclusion principle for an arbitrary parallelogram. What happens if triangle ABC and triangle DEF are acute triangles? obtuse triangles?
2. Construct perpendicular heights in the triangles and apply parts (a) and (b). What happens if triangle ABC and triangle DEF are acute triangles? obtuse triangles?
(e) Prove the gou-gu (Pythagorean) theorem as another application of the inclusion-exclusion principle, following the footsteps of the ancient Chinese. Given right triangle ABC with ∠B a right angle, let a be the length of AB, b the length of CB, and c the length of AC. We wish to prove that
|
First consider the case of an isosceles right triangle, where a = b. By duplicating triangle ABC four times, construct square ACDE (Figure 11).

Figure 11: Square ACDE with a = b.
Explain why the area of this square is c2. Using the area of triangle ABC, explain why square ACDE also has area
|
Now consider right triangle ABC with b > a. Again construct square ACDE with side length c (Figure 12).
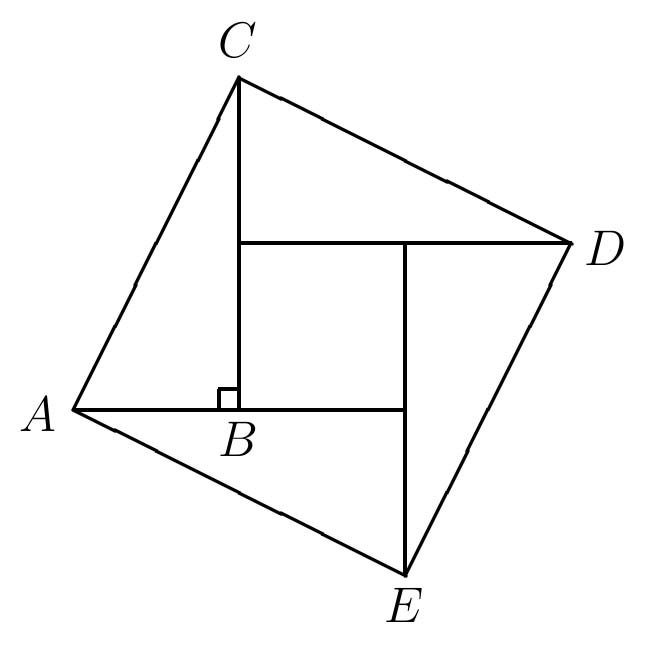
Figure 12: Square ACDE with b > a.
Explain why the inside square has side length b - a. By excluding this inside square from the outside square, find an expression for
|
using two methods, one algebraic, the other geometric in terms of the area of the four remaining triangles. What results after equating these two expressions?
Extra Credit A: Verify the chong cha method by demonstrating that in Figure 3, we have
|
where h is the length of AS, d the length of SN, a1 the length of SB, and a2 the length of ND. Hint: Draw line CK parallel to AB, and consider two pairs of similar triangles, triangles PRA and ASB and triangles PAC and CKD.
Extra Credit B: Read and study Proposition I.43 from the first book of Euclid's Elements. Compare Euclid's use of rigor in the proof of I.43 to the more intuitive application of the "in-out" principle for the rectangle in Figure 5. Speculate why Euclid did not use I.43 to prove VI.4. What may have prevented the ancient Greeks from developing an algebra of real numbers that would have allowed the transfer of results like I.43 to situations like VI.4? What obstacles do incommensurable magnitudes pose in the construction of a real number system?
Jerry Lodder (New Mexico State University), "Proportionality in Similar Triangles: A Cross-Cultural Comparison - The Student Module," Convergence (July 2010)




