- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Solving the Cubic with Cardano - Decomposing a Cube
Decomposing a Cube
In Chapter 6 of the Ars Magna, Cardano presented his decomposition of the cube. Symbolically, this is the familiar \({(x+y)}^3=x^3+3x^2y+3xy^2+y^3,\) but since Cardano wrote before the invention of algebraic symbolism, his presentation was geometric. This presentation was not new with Cardano; it occurred in Fibonacci’s Liber Abaci [Fibonacci, p. 520], a copy of which Cardano had examined in Venice.
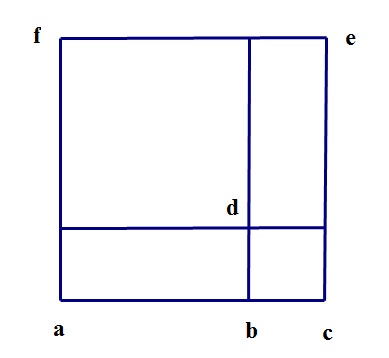
Figure 1. Cardano's figure for cubes.
Figure 1 is my replication of Cardano’s figure in Chapter 12 of the Ars Magna. His figures were all two-dimensional, and his notation for solids and surfaces followed the notation in the diagram. Diagonally opposed points labeled solids and surfaces, as the "cube ae" or the "square ae," and squares and cubes were often referred to by their edges, as “the cube on ac” or “the square on bc.” This figure, then, is the base of a cube, and the line ac does double duty, as an edge of the base and also as the height of the cube.
Breaking the edge ac at the point b triggers the decomposition. This breaks the base into four pieces, as in the figure, while the height ac is broken into two parts, the two line segments ab and bc. Cardano then multiplied each of the four pieces of the base by the two line segments ab and bc, resulting in eight solids. He described the resulting decomposition as [Cardano 1662, p. 251, my translation]:
... the cubes ab and bc, and thrice ab multiplied by the square on bc, and thrice bc multiplied by the square on ab.
The two pictures below present the result.

Figure 2. A cube, with top surface labeled as in Cardano’s diagram.

Figure 3. The cube decomposed.
In Figure 2 above is a cube, marked with Cardano's notation from the image in Chapter 6. In Figure 3 is the same cube, decomposed into its eight pieces. Of course, these are pictures of a particular cube, one with edges of nine units. But the method Cardano described is completely general, and so this particular example stands for all. Cardano's skillful manipulations of the decomposed cube were central to his demonstrations of the solutions to the various cubic problems.
William B. Branson (St. Cloud State University), "Solving the Cubic with Cardano - Decomposing a Cube," Convergence (September 2013), DOI:10.4169/convergence20131001




