- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Sums of Powers of Positive Integers - Abu Bakr al-Karaji (d. 1019), Baghdad
The mathematician Abu Bakr Al-Karaji worked in Baghdad in what is now Iraq for at least part, if not all, of his life. He wrote books on engineering and mathematics, most notably algebra, and died in 1019 (Katz, p. 251).
Al-Karaji stated the result on the sum of the cubes for n = 10 as (using our notation) $$1^3 + 2^3 + 3^3 + \cdots + 10^3 = (1 + 2 + 3 + \cdots + 10)^2, $$
and proved it as follows (Katz, p. 255): If the square shown in Figure 5 has side length 1 + 2 + 3 + · · · + 10, then the square has area (1 + 2 + 3 + · · · + 10)2.
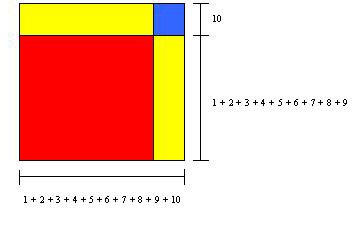
Figure 5. The area of this square can be written in (at least) two different ways.
Likewise, the red square with side length 1 + 2 + 3 + · · · + 9 has area (1 + 2 + 3 + · · · + 9)2. Since each yellow rectangle has area 10(1 + 2 + 3 + · · · + 9) and the blue square has area 102, then the gnomon consisting of the two yellow rectangles and the blue square in Figure 5 has area $$2 \cdot 10(1 + 2 + 3 + \cdots + 9) + 10^2 = 2 \cdot 10 \cdot {{9 \cdot 10} \over 2} + 10^2 = 10 \cdot 10^2 = 10^3. $$
This gives us another way to write the area of the larger square; namely, as the sum of the areas of the red square and of the gnomon, or (1 + 2 + 3 + · · · + 9)2 + 103. Equating our two expressions for the area of the larger square, we have
$$(1 + 2 + 3 + \cdots + 9)^2 + 10^3 =(1 + 2 + 3 + \cdots + 10)^2.$$
Repeating the preceding argument for the square with side length 1 + 2 + 3 + · · · + 9 and a smaller square with side length 1 + 2 + 3 + · · · + 8, we have
$$(1 + 2 + 3 + \cdots + 8)^2 + 9^3 =(1 + 2 + 3 + \cdots + 9)^2.$$
Substituting in the preceding equation, we get
$$(1 + 2 + 3 + \cdots + 8)^2 + 9^3 + 10^3 =(1 + 2 + 3 + \cdots + 10)^2.$$
After repeating the argument seven more times, we obtain
$$1^3 + 2^3 + 3^3 + \cdots + 10^3 = (1 + 2 + 3 + \cdots + 10)^2,$$
al-Karaji’s result.
The mathematican, astronomer, and Biblical scholar Levi ben Gerson (1288-1344), who lived in southern France, gave a similar proof that (1 + 2 + 3 + · · · + n)2 = 13 + 23 + 33 + · · · + n3, which he stated as Proposition 42 in his Maasei Hoshev (The Art of the Calculator), as follows (Katz, pp. 302-304).
The square of the sum of the natural numbers from 1 up to a given number is equal to the sum of the cubes of the numbers from 1 up to the given number. (Katz, p. 304)
The connection given in this formula between sums of cubes and sums of integers might give us hope that the sum of the fourth powers also could be expressed very simply in terms of the sum of integers and/or the sum of squares. Unfortunately, the pattern is not at all transparent, even after writing the formulas for the three sums we’ve considered so far in polynomial form, as follows:
$$1 + 2 + 3 + \cdots + n = {{n^2 } \over 2} + {n \over 2},$$
$$1^2 + 2^2 + 3^2 + \cdots + n^2 = {{n^3 } \over 3} + {{n^2 } \over 2} + {n \over 6},$$
and
$$1^3 + 2^3 + 3^3 + \cdots + n^3 = {{n^4 } \over 4} + {{n^3 } \over 2} + {{n^2 } \over 4}.$$
We can predict that a polynomial formula for
$$1^k + 2^k + 3^k + \cdots + n^k, $$
for k a positive integer, would begin
$${{n^{k + 1} } \over {k + 1}} + {{n^k } \over 2} + \cdots,$$
and, by substituting n = 1 into each side of the equation, we can see that the sum of the coefficients of the polynomial would be 1.
Exercise 7: For n = 4 (rather than n = 10), work through al-Karaji’s argument that (1 + 2 + 3 + 4)2 = 13 + 23 + 33 + 43 in three steps, illustrating each step using the same large square. The left side of the equation is the height times the width of this large square, hence is its area. Which regions of the large square does the right side of the equation represent? That is, of which region of the large square does each of the four terms in the right side of the equation give the area? Hint: Gnomons!
Exercise 8: According to the last sentence of the section, what are the possible polynomial formulas for the sum of the fourth powers, 14 + 24 + 34 + · · · + n4? List three possibilities.
For solutions to these exercises, click here.
Janet Beery (University of Redlands), "Sums of Powers of Positive Integers - Abu Bakr al-Karaji (d. 1019), Baghdad," Convergence (July 2010), DOI:10.4169/loci003284




