- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Sums of Powers of Positive Integers - Solutions to Exercises 1-3
Exercise 1.
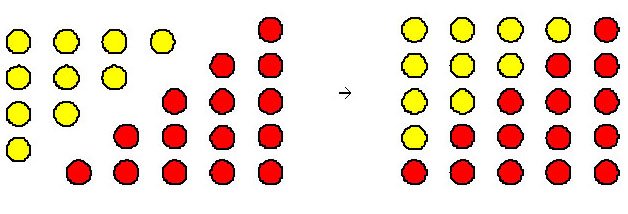
Figure 12. The sum of the 4th and 5th triangular numbers is the 5th square number.
Figure 12 illustrates that the sum of the 4th and 5th triangular numbers is the 5th square number (or the square of side length 5), or that 10 + 15 = 25 = 52. That 6 + 10 = 16 = 42 and 15 + 21 = 36 = 62 can be illustrated in similar fashion. The general relationship can be expressed as Tn + Tn+1 = (n+1)2, where Tn is the nth triangular number, or, since Tn = n(n + 1)/2, as $${{n(n + 1)} \over 2} + {{(n + 1)(n + 2)} \over 2} = (n + 1)^2.$$
The latter equation can be checked easily using algebra.
Exercise 2.
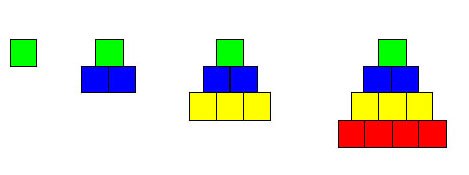
Figure 13. The first four triangular numbers represented using squares
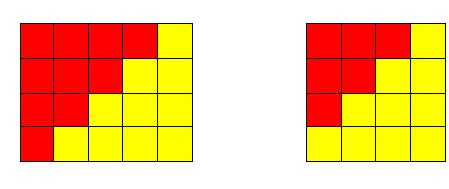
Figure 14. The identity \( 1 + 2 + 3 + ... + n = \frac{n(n + 1)}{2}\) for n = 4 (left),
and the identity from Exercise 1 for n = 3 (right)
Exercise 3. Six pyramids constructed of 1 + 3 + 6 + 10 = 20 cubes each can be fitted together to form a rectangular solid of dimensions 4 x 5 x 6, or 120 cubes in all, as shown in Figure 15. This construction illustrates that 6(1 + 3 + 6 + 10) = 4 x 5 x 6 or that \( 1 + 3 + 6 + 10 = \frac{4\times 5\times 6}{6}.\) In general, we have $$6\left( {1 + 3 + 6 + \cdots + {{n(n + 1)} \over 2}} \right) = n(n + 1)(n + 2)$$ or $$1 + 3 + 6 + \cdots + {{n(n + 1)} \over 2} = {{n(n + 1)(n + 2)} \over 6}.$$
Janet Beery (University of Redlands), "Sums of Powers of Positive Integers - Solutions to Exercises 1-3," Convergence (July 2010), DOI:10.4169/loci003284




