- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Sums of Powers of Positive Integers - Solutions to Exercises 13-14
Exercise 13. The constant difference table for sums of fifth powers is in Figure 20. Blue entries are obtained from knowing that the next highest entry in the fifth powers column is 0; that is, from knowing that 05 = 0. Red entries are obtained from knowing the constant difference is 120. Blue entries may be obtained in this way, too.
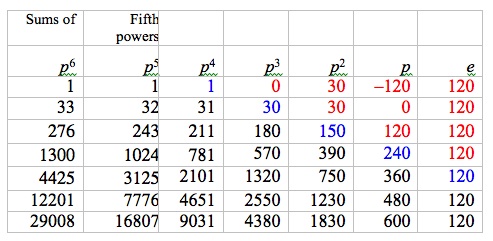
Figure 20. Constant difference table for sums of fifth powers
Substituting the values from the first row of the table in Figure 20 into Harriot’s formula for v6, we obtain the following:
$$\eqalign{720 v^6 &= 120nnnnnn + 1080nnnnn + 3000nnnn + 1800nnn - 3120nn - 2880n \cr & \quad \quad \quad \quad \quad \quad \;\;\; - 720nnnnn - 3600nnnn - 3600nnn + 3600nn + 4320n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \;\;\; + 900nnnn + 1800nnn - 900nn - 1800n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; + 0nnn\;\;\; - 0nn\;\;\; - 0n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \quad \quad \quad \quad \quad \; + 360nn - 360n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \;\quad \quad \quad \quad \quad \quad \quad \quad \quad + 720n - 720 \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; + 720\cr & = 120nnnnnn + 360nnnnn + 300nnnn + 0nnn - 60nn + 0n + 0\cr &= 120nnnnnn + 360nnnnn + 300nnnn - 60nn,}$$ or $$v^6 = {1 \over {720}}\left( {120nnnnnn + 360nnnnn + 300nnnn - 60nn} \right)$$ $$= {1 \over 6}nnnnnn + {1 \over 2}nnnnn + {5 \over {12}}nnnn - {1 \over {12}}nn,$$
or, in modern notation,
$$\sum_{k = 1}^n {k^5 } = {1 \over 6}n^6 + {1 \over 2}n^5 + {5 \over {12}}n^4 - {1 \over {12}}n^2.$$
Exercise 14.
We have
$$\eqalign{v^5 = & {{(n + 3)(n + 2)(n + 1)n(n - 1)} \over {5 \cdot 4 \cdot 3 \cdot 2}}e + {{(n + 2)(n + 1)n(n - 1)} \over {4 \cdot 3 \cdot 2}}p\cr & + {{(n + 1)n(n - 1)} \over {3 \cdot 2}} p^2 + {{n(n - 1)} \over {2}} p^3 + (n - 1) p^4 + p^5,}$$
$$\eqalign{v^6 & = {{(n + 4)(n + 3)(n + 2)(n + 1)n(n - 1)} \over {6 \cdot 5 \cdot 4 \cdot 3 \cdot 2}}e + {{(n + 3)(n + 2)(n + 1)n(n - 1)} \over {5 \cdot 4 \cdot 3 \cdot 2}}p\cr &+ {{(n + 2)(n + 1)n(n - 1)} \over {4 \cdot 3 \cdot 2}} p^2 + {{(n + 1)n(n - 1)} \over {3 \cdot 2}} p^3 + {{n(n - 1)} \over 2} p^4 + (n - 1) p^5 + {p^6},}$$ and
$$\eqalign{v^7 & = {{(n + 5)(n + 4)(n + 3)(n + 2)(n + 1)n(n - 1)} \over {7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2}}e\cr & + {{(n + 4)(n + 3)(n + 2)(n + 1)n(n - 1)} \over {6 \cdot 5 \cdot 4 \cdot 3 \cdot 2}}p + {{(n + 3)(n + 2)(n + 1)n(n - 1)} \over {5 \cdot 4 \cdot 3 \cdot 2}} p^2\cr & + {{(n + 2)(n + 1)n(n - 1)} \over {4 \cdot 3 \cdot 2}} p^3 + {{(n + 1)n(n - 1)} \over {3 \cdot 2}} p^4 + {{n(n - 1)} \over 2} p^5 + (n - 1) p^6 + p^7}$$ or $$v^7 = {n+5\choose 7}e + {n+4\choose 6}p + {n+3\choose 5}p^2 + {n+2\choose 4}p^3 + {n+1\choose 3}p^4$$
\(\displaystyle{+ {n \choose 2}p^5 + (n - 1) p^6 + p^7.}\)
Janet Beery (University of Redlands), "Sums of Powers of Positive Integers - Solutions to Exercises 13-14," Convergence (July 2010), DOI:10.4169/loci003284




