- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Best Known Old Babylonian Tablet?
About YBC 7289

Figure 1. YBC 7289 is an ancient Mesopotamian clay tablet with interesting and important mathematical content. (Photograph used with the permission of the Yale Babylonian Collection. Personal classroom use permitted; all other uses require permission from the Yale Babylonian Collection.)
YBC 7289 is an Old Babylonian clay tablet (circa 1800–1600 BCE) from the Yale Babylonian Collection. A hand tablet, it appears to be a practice school exercise undertaken by a novice scribe. But, mathematically speaking, this second millennium BCE document is one of the most fascinating extant clay tablets because it contains not only a constructed illustration of a geometric square with intersecting diagonals, but also, in its text, a numerical estimate of \(\sqrt 2\) correct to three sexagesimal or six decimal places. The value is read from the uppermost horizontal inscription and demonstrates the greatest known computational accuracy obtained anywhere in the ancient world. It is believed that the tablet’s author copied the results from an existing table of values and did not compute them himself. The contents of this tablet were first translated and transcribed by Otto Neugebauer and Abraham Sachs in their 1945 book, Mathematical Cuneiform Texts (New Haven, CT: American Oriental Society). More recently, this tablet was the subject of an article by David Fowler and Eleanor Robson [3], which provides insights into the probable methodology used to obtain such an accurate approximation for \(\sqrt 2.\)
An excellent summary of the tablet's content and context is available from Duncan Melville's Mesopotamian Mathematics website. His "Tablets on the Web" pages include one on YBC 7289 [4]. Bill Casselman's website [2] contains additional analysis and photographs. Begin with his YBC 7289 Main Page or go straight to his Analysis of YBC 7289 for instructions on how to read the tablet's cuneiform text.
YBC 7289 was acquired by Yale University from the estate of the 19th century industrialist J. P. Morgan. The image of YBC 7289 in Figure 1 is presented with the permission of the Yale Babylonian Collection and the assistance of Ulla Kasten, Associate Curator of the Collection.
YBC 7289 in the Classroom
When Frank Swetz sent me an image of YBC 7289, the Old Babylonian tablet displayed in Figure 1 above, to share with Convergence readers, I smiled with some sense of satisfaction. This was because, just this past May term, after many years of trying, I felt I finally had honed to as-good-as-it-would-get my presentation of the contents of this tablet to my liberal arts mathematics history students. The ideal I had in mind all these years was to design an activity in which students deciphered the tablet, discovered for themselves Old Babylonian (or, more generally, ancient Mesopotamian) base 60 fractions, figured out that one of the numbers on the tablet approximated the value we denote as \(\sqrt 2,\) and completed all three of these tasks well within 50 minutes.
As is often the case in matters of teaching and learning, the breakthrough came when I gave up some of my aspirations, deciding that it wasn’t so important that students deciphered the tablet themselves or – and this was the hardest goal to give up – that they completed the remaining parts of the exercise in small groups without much assistance from me. After long experience, I finally admitted that, in order to complete this exploration in a reasonable amount of time with every student understanding the mathematical ideas, I probably needed to lead the discussion.
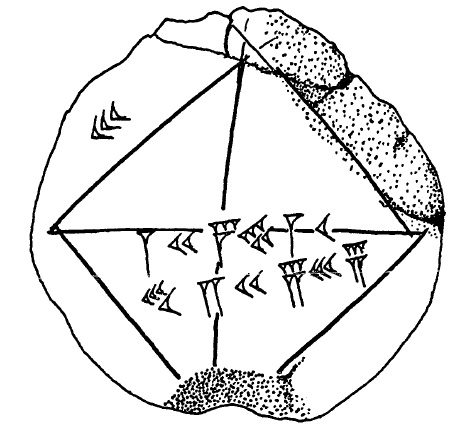
Figure 2. This sketch of the tablet appears on page 27 of the book by Aaboe [1], and is reproduced here courtesy of the Mathematical Association of America (MAA).
Coming into this discussion, my 30+ students knew how to represent whole numbers using Mesopotamian cuneiform fairly well and how to use the Pythagorean Theorem quite well. They also had some recent experience with fractions in the form of ancient Egyptian unit fractions, but no experience with Mesopotamian fractions. After seeing photographs of the tablet itself and receiving their own copies of the drawing by Aaboe [1, p. 27] in Figure 2 above (which I also projected using a document camera or drew on the board – I don’t remember which), they could make their “best guesses” of the digits making up the three numbers shown in the diagram as \(30\) in the upper left; \(1, 24, 51, 10\) along the horizontal diagonal; and \(42, 25, 35\) in the lower half of the figure. What I mean by “best guesses” is that students knew that the digits along the horizontal, for instance, might be read as, say, \(1, 0, 20, 4, 51, 10, 0, 0,\) but that \(1, 24, 51, 10\) would be more likely without additional context. Their best guesses as to the numbers themselves then would have been \[30\times 1 = 30,\] \[1\times 60^3 + 24\times 60^2 + 51\times 60 + 10\times 1 = 305470,\] and \[42\times 60^2 + 25\times 60 + 35\times 1 = 152735.\]
We agreed that, if the diagram was indeed a square, then the length of each of its sides and, in particular, of its upper righthand side, would be \(30.\) I then asked which of the two numbers along the diagonal was its length. Some students said that both numbers were too large to be the length of the diagonal of a square of side length \(30.\) I asked the class to compute the length of the diagonal by focusing on the triangle making up the upper half of the square – that is, I hid the lower half of the square until several students noted that the upper half formed a right triangle with its hypotenuse formed by the diagonal in question. Students then used the Pythagorean Theorem to compute the length of the diagonal rounded to 6 places after the decimal point, obtaining \(d = \sqrt{30^2 + 30^2} = 42.426407.\) They noticed that there was also a \(42\) among the digits of the Mesopotamian numbers, but were otherwise stymied. My hint was to consider what \(42.426407\) represents to us; namely, \[4\times 10 + 2\times 1 + 4\times {\frac{1}{10}} + 2\times {\frac{1}{100}} + 6\times {\frac{1}{1000}} + 4\times {\frac{1}{10000}} + \cdots\] or \[4\times 10^1 + 2\times 10^0 + 4\times {\frac{1}{10^1}} + 2\times {\frac{1}{10^2}} + 6\times {\frac{1}{10^3}} + 4\times {\frac{1}{10^4}} + \cdots\] or \[4\times 10^1 + 2\times 10^0 + 4\times {10^{-1}} + 2\times {10^{-2}} + 6\times {10^{-3}} + 4\times {10^{-4}} + \cdots.\]
This hint was enough to prompt students (after we all enjoyed an “aha!” moment together) to begin writing the number \(42, 25, 35\) from the tablet as \[42\times 1 + 25\times {\frac{1}{60}} + 35\times {\frac{1}{3600}},\] with some students requiring help from their neighbors to write the last summand – and with some students preferring \(35\times {\frac{1}{60^2}}\) or \(35\times {60^{-2}}\). I then asked if this number was \(42.426407\) and, with some reminders on how to enter sums of fractions into their calculators without losing accuracy, they reported that \[42\times 1 + 25\times {\frac{1}{60}} + 35\times {\frac{1}{3600}} = 42.426389\] when rounded to 6 places after the decimal point, which agreed with \(42.426407\) when rounded to 4 places after the decimal point.
I then asked the students what the remaining number on the tablet could be. They were hesitant to experiment, so one way to proceed might have been to assign half the class to convert \(1; 24, 51, 10\) to decimal and the other half to convert \(1, 24; 51, 10\) to decimal and both groups to multiply their result by \(30.\) Instead, I reminded the class that I would compute the length of the diagonal as \[d = \sqrt{30^2 + 30^2} = \sqrt{2\cdot 30^2} = 30\sqrt 2\approx 42.426407\] and asked them to compute \(\sqrt 2\) on their calculators. On seeing that \(\sqrt 2 \approx 1.414214,\) students converted \(1; 24, 51, 10\) to \[1 + \frac{24}{60} + \frac{51}{3600} + \frac{10}{216000}\approx 1.414213,\] which, as I excitedly pointed out, is an approximation to \(\sqrt 2\) accurate to 5 digits after the decimal point.
But what could the author of the tablet be trying to tell us? In answer to this question and with our diagram labeled with \(30\) and \(30\sqrt 2\) in appropriate places, at least a few students concluded that the tablet might be interpreted as saying that, given a square of side length \(30\) (or a right triangle with both legs of length \(30\)), in order to obtain the length of the diagonal (or the hypotenuse), multiply \(30\) by \(1; 24, 51, 10\) or \({\sqrt 2},\) and, more generally, given any side (or leg) length, multiply it by \(1; 24, 51, 10\) in order to get the length of the diagonal (or hypotenuse). If I had not already done so, at this point, I would have shared that Assyriologists (= modern scholars of ancient Mesopotamia) believe the tablet to be an erasable tablet used by a student in scribal school. Definitely at this point, I shared that these scholars believe the exercise assigned to the scribal school student to have been, given a square of side length \(30,\) find the length of the diagonals of the square by either remembering or looking up in a table the correct constant by which to multiply the side length in order to get the diagonal length. In fact, according to Fowler and Robson:
This approximation to \(\sqrt 2\) would have been copied by the scribe from a so-called coefficient list – a list of numbers useful for doing calculations. These reference lists were a vital part of Mesopotamian mathematics. [3, p. 370]
At some point, I introduced the notation \(42; 25, 35\) for the base 60 number \[42\times {60^{0}} + 25\times {60^{-1}} + 35\times {60^{-2}}\] (even though \(42. 25, 35\) would make more sense to American students). Students were not too surprised to learn that one most often determines where the sexagesimal point goes by guessing from context because they had already learned this to be true for whole numbers.
There are many directions in which to proceed from here, with perhaps the most interesting being to multiply the sexagesimal numbers \(30\) and \(1; 24, 51, 10\) together without converting to decimal. This is a skill that my best students almost always figure out on their own, and that the entire class usually ends up discussing because invariably one of the students who worked it out for herself will present it to the class (often for base 20 instead of base 60) as a step in solving another problem. It’s even more fun when these students try to add and multiply Maya calendar numbers, in which the place that would be \(20^2\) in a base 20 system is instead \(18\times 20\) (and the next place \(20\times 18\times 20\) and so on), but I digress. Another direction would be to focus on interpretation of the digit \(30\) as \(0; 30 =\frac{30}{60}\) or \({\frac{1}{2}},\) in which case the remaining two numbers on the tablet would be \({\sqrt 2}\) and \(\frac{1}{\sqrt 2}\) (see references [3] and [4] for brief discussions of Mesopotamian interest in reciprocals). One also could discuss how the Mesopotamians obtained their estimate of \({\sqrt 2}\) (see [3] for one possible answer). This year, one of my students subsequently made a presentation on Ptolemy’s table of chords, so we were reminded of our base 60 convention for minutes and seconds when measuring angles (arcs for Ptolemy) in degrees.
Although it would be quick (15 minutes or less) and fun to make a presentation like the one described above to mathematics majors and minors, these students can complete this exercise on their own or in small groups without much assistance. I am not convinced that deciphering the text from a photo of the tablet itself is worth their time, but, given the same prerequisite knowledge of Mesopotamian base 60 whole numbers, the drawing from Aaboe’s book, and a few leading questions, they can figure out on their own essentially what’s going on in this tablet and hence be prepared for reading and/or discussion of Assyriologists’ current knowledge of Old Babylonian coefficient lists, including how Mesopotamians may have made this approximation of \(\sqrt 2\) in the first place. Besides being an excellent reference for instructors, the article by Fowler and Robson [3] makes a good – and free! – reading assignment for these students.
[1] Aaboe, Asger, Episodes from the Early History of Mathematics, Washington, D.C.: MAA, 1998 (originally published in 1964), especially pp. 25-27.
[2] Casselman, Bill, YBC 7289 Main Page and Analysis of YBC 7289 (University of British Columbia). These webpages contain additional photographs and analysis, including instructions for how to read the cuneiform text.
http://www.math.ubc.ca/~cass/Euclid/ybc/ybc.html
[3] Fowler, D. H. and E. R. Robson (1998). Square root approximations in Old Babylonian mathematics: YBC 7289 in context. Historia Mathematica 25, 366-378.
http://math.berkeley.edu/%7Elpachter/128a/Babylonian_sqrt2.pdf
[4] Melville, Duncan, Mesopotamian Mathematics: Tablets on the Web: YBC 7289 (St. Lawrence University). This webpage contains the images from our Figures 1 and 2, along with analysis.
http://it.stlawu.edu/~dmelvill/mesomath/tablets/YBC7289.html
About the Authors
Frank Swetz is founding editor (along with Victor Katz) of Convergence and Janet Beery is its current editor (with Kathy Clark). Swetz and Katz are the authors of the Convergence feature Mathematical Treasures, and Swetz will continue to collect "mathematical treasures" for Convergence from important libraries in the United States during 2012 and beyond.
Janet L. Beery (University of Redlands) and Frank J. Swetz (The Pennsylvania State University), "The Best Known Old Babylonian Tablet?," Convergence (July 2012), DOI:10.4169/loci003889




