- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Geometry of Rene Descartes
In 1637, the French philosopher and mathematician René Descartes (1596–1650) published his Discours de la methodé (see the title page) in which he explained his rationalist approach to the interpretation of nature. La methodé contained three appendices: La dioptrique, Les météories, and La géométrie. The last of these, The Geometry, was Descartes’ only published mathematical work.

Figure 1. Frontispiece of 1659 Latin edition of Descartes’ Geometry showing a portrait of the author, René Descartes
Approximately 100 pages in length, The Geometry was not a large work, but it promised a new approach in mathematical thinking. Descartes boasted in his introduction that “Any problem in geometry can easily be reduced to such terms that a knowledge of the length of certain straight lines is sufficient for construction." He then proceeded to show how arithmetic, algebra, and geometry could be combined to solve problems. After defining a unit length, Descartes demonstrated procedures for adding, subtracting, multiplying, and dividing line segments and for graphically determining roots of equations. But Descartes’ La géométrie was difficult to understand and follow. It was written in French, not the language of scholarly communication at the time, and Descartes' writing style was often obscure in its meaning.

Figure 2. Title page of van Schooten’s 1659 Latin edition of Descartes’ Geometry
In 1649, Frans van Schooten (1615–1660), a Dutch mathematician, published a Latin translation of Descartes’ Geometry, adding his own clarifying explanations and commentaries. Descartes’ friend and colleague, Florimond de Beaune (1601–1652), contributed an introduction to this edition. Van Schooten published a second edition in 1659, providing even more explanation and commentary. Now the message of Descartes’ Geometry was available to a large reading audience, and it became an influential work, spurring on the development of analytic geometry.
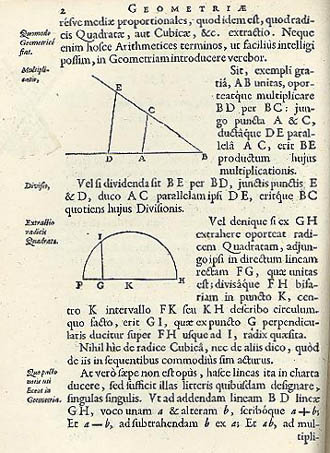
Figure 3. On Page 2 of the Latin edition of Descartes’ Geometry, the author demonstrated, in the uppermost illustration, the procedure for obtaining the product of two given line segments, BD and BC. A unit length AB is designated. Then when DE is constructed parallel to AC, it is found that BD x BC = AB x BE. However, AB is the unit length; therefore BD x BC = BE.
Additional Resources
Descartes’ Geometry in English:
The Geometry of Rene Descartes (translated by David Eugene Smith and Marcia Latham), first published by Open Court in 1925 and by Dover in 1954
Discourse on the Method, …, The Geometry, in Great Books of the Western World (2nd edition), vol. 28, Encyclopaedia Britannica, Chicago, 1990-1991
Discourse on Method, Optics, Geometry, and Meteorology (translated by Paul Olscamp), Bobbs-Merill, Indianapolis, 1965; revised edition, Hackett Publishing, Indianapolis, 2001
Descartes’ Geometry in French:
The complete text of Rene Descartes’ La géométrie in French is available courtesy of Project Gutenberg.
An 1886 edition of La géométrie de Rene Descartes published in Paris can be viewed courtesy of the Cornell University Library.
Descartes’ Geometry in Latin:
First, second, and third editions of Frans van Schooten’s Latin Geometria a Renato Des Cartes from 1649, 1659 and 1683, respectively, can be viewed at Google Books by searching for “Rene Descartes Geometria” and “Renato Descartes Geometria”.
About Descartes and his mathematics:
Victor J. Katz, A History of Mathematics (3rd ed.), Addison-Wesley, Boston, 2009
About Descartes and his science:
William R. Shea, The Magic of Numbers and Motion: The Scientific Career of Rene Descartes, Science History Publications, Watson Publishing International, Canton, Massachusetts, 1991
Frank J. Swetz (The Pennsylvania State University), "The Geometry of Rene Descartes," Convergence (March 2010), DOI:10.4169/loci003444




