- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Quadrature of the Circle and Hippocrates' Lunes - Hippocrates' Lunes
[From Joannes Philoponus, In Aristotelis Physica.]32
Hippocrates of Chios was a merchant who fell in with a pirate ship and lost all his possessions. He came to Athens to prosecute the pirates and, staying a long time in Athens by reason of the indictment, consorted with philosophers, and reached such proficiency in geometry that he tried to affect the quadrature of the circle. He did not discover this, but having squared the lune he falsely thought from this that he could square the circle also. For he thought that from the quadrature of the lune the quadrature of the circle could also be calculated.33
[From Simplicius, In Aristotelis Physica.]34
Eudemus,35 however, in his History of Geometry says that Hippocrates did not demonstrate the quadrature of the lune on the side of a square36 but generally, as one might say.37 For every lune has an outer circumference equal to a semicircle or greater or less, and if Hippocrates squared the lune having an outer circumference equal to a semicircle and greater and less, the quadrature would appear to be proved generally.38 I shall set out what Eudemus wrote word for word, adding only for the sake of clearness a few things taken from Euclid's Elements on account of the summary style of Eudemus, who set out his proofs in abridged form in conformity with the ancient practice. He writes thus in the second book of the History of Geometry:
The quadratures of lunes, which seemed to belong to an uncommon class of propositions by reason of the close relationship to the circle, were first investigated by Hippocrates, and seemed to be set out in correct form; therefore we shall deal with them at length and go through them. He made his starting-point, and set out as the first of the theorems useful to this purpose, that similar segments of circles have the same ratios as the squares on their bases.39 And this he proved by showing that the squares on the diameters have the same ratios as the circles.40 Having first shown this he described in what way it was possible to square a lune whose outer circumference was a semicircle. He did this by circumscribing about a right-angled isosceles triangle a semicircle and about the base a segment of a circle similar to those cut off by the sides.41 Since the segment about the base is equal to the sum of those about the sides,42 it follows that when the part of the triangle above the segment about the base is added to both, the lune will be equal to the triangle.43
Therefore the lune, having been proved equal to the triangle, can be squared. In this way, taking a semicircle as the outer circumference of the lune, Hippocrates readily squared the lune.
Footnotes:
32Philoponus was a sixth century CE philosopher and Christian theologian who studied the works of Greek philosophers, especially those of Aristotle, and wrote extensive commentaries on them. This excerpt comes from a commentary on Aristotle's Physics. A native of Egyptian Alexandria, he lives at the end of the period of Greek progress in the sciences.
33We will analyze in detail Hippocrates' quadrature of one type of lune in the next text below. It is enough for now to understand the point Philoponus makes here concerning the quadrature of the circle. For Hippocrates' work represented the first time that someone had determined the area of a figure with curved sides - in fact, with circular sides - and it was thought that the techniques he used for the quadrature of the lune might lead to a positive resolution to the quadrature of the circle. Alas, as we shall see below, this was never to be!
34Simplicius was another sixth century commentator on early Greek texts, notably on the works of Aristotle and Euclid. He was born in Cilicia, a Roman province which is today part of Turkey. He studied in Alexandria under a pupil of Proclus, and also at Athens at Plato's Academy.
35Eudemus of Rhodes lived in the late fourth century BCE and was the first historian of mathematics. He was a fellow student with Aristotle in Athens and authored histories of geometry, arithmetic and astronomy, none of which survive today. What we know of his work is based on references and quotes in other works like this commentary on Aristotle's Physics by Simplicius. Here Simplicius quotes from Eudemus' history of geometry. Because Eudemus is writing so much closer in time to Hippocrates and the other Greek geometers, he is considered a valuable historical source.
36By this, Simplicius means the quadrature of the lune constructed as follows: given a circle and an inscribed square, build the circle whose diameter is one of the sides of the square. The lune being described here is the one inside the second smaller circle and outside the larger.
37Simplicius seems to believe that Hippocrates had claimed to have successfully squared the circle as a result of his work on lunes, but the argument he gives does not accomplish this, so Simplicius is not to be trusted on this account.
38A lune has two boundary arcs; the line segment that joins the endpoints of these arcs forms a chord in each of the two circles. Simplicius is here describing the situation in which the arc of the outer circle is a semicircle, or is less than a semicircle, or more than a semicircle. If Hippocrates had successfully worked out the quadrature of the lune in all these cases, then by arranging that the outer arc of the lune increases to its greatest possible extent and the inner arc shrinks to a point, then the lune becomes a full circle and the quadrature of the circle would be resolved!
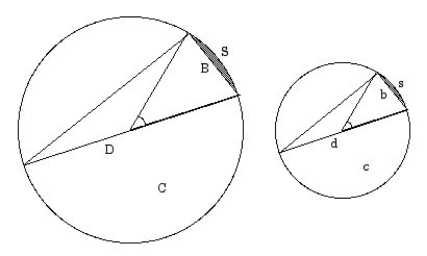
39A segment of a circle is any portion of the circle cut off by a single line. Segments are similar if the arcs that bound them come from equal central angles in their respective circles (the shaded areas labeled s and S in the figure below).
Thus, to say that "similar segments of circles have the same ratios as the squares on their bases" means that the ratio of the areas of the segments is the same as the ratio of the squares of the lengths of their straight line bases. In symbols, if one segment s has base b and the other segment S has base B, then
|
40This result (Elements, XII.2) is the key idea behind this quadrature. It says that if one circle c has diameter d and another circle C has diameter D, then
|
Draw the diameter d through one of the endpoints of b, then complete the triangle two of whose sides are b and d. (Refer to Figure 7.) Similarly, in circle C, draw diameter D through one of the endpoints of B, then complete the triangle two of whose sides are B and D. Then, on the one hand, similarity of the segments means that segment s is the same fraction of circle c that segment S is of circle C, or
|
|
|
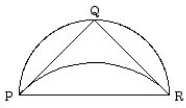
41The semicircle circumscribed around the right triangle in Figure 9 forms the outer circumference of the lune. The inner circumference is formed by the arc of a second circle that makes a segment with the base PR of the triangle similar to the two segments between the semicircle and the other two sides PQ and QR of the triangle. Each of these three segments cuts off a 90 degree arc from its circle.
Simplicius described this lune as one ön the side of a square." To see that he is talking about the same lune as the one described by Eudemus, consider from the diagram below the entire circle that forms the inner circumference of this lune. The base of the semicircle that forms the outer circumference of the lune is one side of a square that can be inscribed in this inner circle. Thus, the lune can be seen to rest on neighboring vertices of a square inscribed in the circle that forms its inner circumference.

Figure 10
42This is determined by combining the result on ratios of similar segments with the Pythagorean theorem. Referring to this figure, the Pythagorean theorem says that (PQ)2 + (QR)2 = (PR)2. But b = PQ = QR is the common length of the base of the two small segments, and B = PR is the length of the base of the larger segment, so we can express this relation as b2 + b2 = B2, or in terms of ratios,
|
|
43Hippocrates' lune is comprised of both of the two small circular segments and the isosceles right triangle (see Figure 9). Since the sum of the two small segments is equal to the one larger one, and replacing the two smaller areas with the larger one produces the triangle PQR, Hippocrates has therefore shown that the lune equals the triangle!
Daniel E. Otero (Xavier University), "The Quadrature of the Circle and Hippocrates' Lunes - Hippocrates' Lunes," Convergence (July 2010)




