- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Quadrature of the Circle and Hippocrates' Lunes - The Quadrature of Polygons in Euclid's Elements, Books I, II
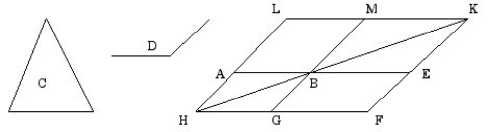
[Proposition I.44.] To a given straight line in a given rectilinear angle, to apply a parallelogram equal to a given triangle.13
Let AB be the given straight line, D the given rectilinear angle, and C the given triangle.
It is required to apply a parallelogram equal to the given triangle C to the given straight line AB in an angle equal to D.
Construct the parallelogram BEFG equal to the triangle C in the angle EBG which equals D, and let it be placed so that BE is in a straight line with AB.14
Draw FG through to H, and draw AH through A parallel to either BG or EF. Join HB.
Since the straight line HF falls upon the parallels AH and EF, therefore the sum of the angles AHF and HFE equals two right angles.15 Therefore the sum of the angles BHG and GFE is less than two right angles. And straight lines produced indefinitely from angles less than two right angles meet, therefore HB and FE, when produced, will meet.16
Let them be produced and meet at K. Draw KL through the point K parallel to either EA or FH. Produce HA and GB to the points L and M.17
Then HLKF is a parallelogram, HK is its diameter,18 and AG and ME are parallelograms, and LB and BF are the so-called complements about HK. Therefore LB equals BF.19
But BF equals the triangle C, therefore LB also equals C.
Since the angle GBE equals the angle ABM, while the angle GBE equals D, therefore the angle ABM also equals the angle D.
Therefore the parallelogram LB equal to the given triangle C has been applied to the given straight line AB, in the angle ABM which equals D. QEF
[Proposition I.45.] To construct a parallelogram equal to a given rectilinear figure in a given rectilinear angle.
Let ABCD be the given rectilinear figure and E the given rectilinear angle.
It is required to construct a parallelogram equal to the rectilinear figure ABCD in the given angle E.
Join DB. Construct the parallelogram FH equal to the triangle ABD in the angle HKF which equals E.20 Apply the parallelogram GM equal to the triangle DBC to the straight line GH in the angle GHM which equals E.21
Since the angle E equals each of the angles HKF and GHM, therefore the angle HKF also equals the angle GHM.
Add the angle KHG to each. Therefore the sum of the angles FKH and KHG equals the sum of the angles KHG and GHM.
But the sum of the angles FKH and KHG equals two right angles, therefore the sum of the angles KHG and GHM also equals two right angles.
Thus, with a straight line GH, and at the point H on it, two straight lines KH and HM not lying on the same side make the adjacent angles together equal to two right angles, therefore KH is in a straight line with HM.22
Since the straight line HG falls upon the parallels KM and FG, therefore the alternate angles MHG and HGF equal one another.
Add the angle HGL to each. Then the sum of the angles MHG and HGL equals the sum of the angles HGF and HGL.
But the sum of the angles MHG and HGL equals two right angles, therefore the sum of the angles HGF and HGL also equals two right angles. Therefore FG is in a straight line with GL.23
Since FK is equal and parallel to HG, and HG equal and parallel to ML also, therefore KF is also equal and parallel to ML, and the straight lines KM and FL join them at their ends. Therefore KM and FL are also equal and parallel. Therefore KFLM is a parallelogram.
Since the triangle ABD equals the parallelogram FH, and DBC equals GM, therefore the whole rectilinear figure ABCD equals the whole parallelogram KFLM.
Therefore the parallelogram KFLM has been constructed equal to the given rectilinear figure ABCD in the angle FKM which equals the given angle E. QEF
[Proposition II.14.] To construct a square equal to a given rectilinear figure.
Let A be the given rectilinear figure.

Figure 6: Elements, II.14.
It is required to construct a square equal to the rectilinear figure A.
Construct the rectangular parallelogram BD equal to the rectilinear figure A.24
Then, if BE equals ED, then that which was proposed is done, for a square BD has been constructed equal to the rectilinear figure A.25
But, if not, one of the straight lines BE or ED is greater. Let BE be greater, and produce it to F. Make EF equal to ED, and bisect BF at G.26
Describe the semicircle BHF with center G and radius one of the straight lines GB or GF. Produce DE to H, and join GH.
Then, since the straight line BF has been cut into equal segments at G and into unequal segments at E, the rectangle BE by EF together with the square on EG equals the square on GF.27
But GF equals GH, therefore the rectangle BE by EF together with the square on GE equals the square on GH.
But the sum of the squares on HE and EG equals the square on GH,28 therefore the rectangle BE by EF together with the square on GE equals the sum of the squares on HE and EG.
Subtract the square on GE from each. Therefore the remaining rectangle BE by EF equals the square on EH.
But the rectangle BE by EF is BD, for EF equals ED, therefore the parallelogram BD equals the square on HE.
And BD equals the rectilinear figure A.29
Therefore the rectilinear figure A also equals the square which can be described on EH.
Therefore a square, namely that which can be described on EH, has been constructed equal to the given rectilinear figure A. QEF
Footnotes:
13For Euclid, a "straight line" means a line segment with endpoints, not an infinitely long line. Notice also the special use of the verb "apply," meaning to build with a given segment as side.
14Here Euclid uses the result of I.42.
15In modern geometry, we would say that angles AHF and HFE are supplementary, that is, they add up to 180°. But Euclid never uses the degree as a unit of angular measure. Instead, he measures all angles in reference to the right angle as the basic unit. Here he needs to make use of the fact, which he proves in I.29, that alternate interior angles made by a transversal line across a pair of parallels are supplementary to each other.
16It is clear from the diagram that these lines meet, but Euclid proves this, since he is careful not to rely on the drawing for his argument. After all, the drawing represents a typical, but not universal, situation. Since angle BHG is certainly smaller than AHG, the angles BHG and GFE sum to less than 180°. It follows then (from the famous Parallel Postulate) that the lines HB and FE are not parallel and must meet.
17It is curious that, after going through the trouble to argue why HB and FE must meet at a point K, Euclid does not explain how he knows that HA and GB, when produced, will eventually cut KL in points L and M, respectively. Mathematicians of the nineteenth century studied Euclid's proof-writing techniques carefully and recognized that he wasn't always as rigorous as he could have been. Still, the issue at this point in his proof is not a serious one. One can, if necessary, provide a more complete proof that fills in this small lacuna in the logic.
18A diameter of a parallelogram corresponds to either of the diagonal lines joining opposite corners of the figure.
19Parallelograms, rectangles and squares are often labeled by Euclid by referring to a pair of opposite corners of the figure. In the diagram accompanying this proposition, the large parallelogram HLKF has been divided into four smaller parallelograms, two straddling the diameter HK, namely AG and ME, and two others, LB and BF, called complements by Euclid.
Since the diameter of a parallelogram cuts the figure in half, into two congruent triangles, it follows that triangles HLK and KFH are equal, as are HAB and BGH, and BMK and KEB. Removing HAB and BMK from HLK leaves parallelogram LB, and removing BGH and KEB from KFH leaves parallelogram BF, so these paralleograms are equal as well.
20Here Euclid uses Proposition I.42.
21Here he uses Proposition I.44.
22While it may seem apparent from the diagram that HM is a simple extension of the line KH, it was not added to the diagram as an extension of this line, so Euclid must prove that it is so, which he does by showing that angle KHM is a 180°angle.
23This mirrors the argument above to show that angle FGL is a 180°angle.
24Finally, Euclid has accumulated the machinery he needs, in the guise of the propositions we have worked through above, to solve the problem central to our discussion here, the quadrature of any polygonal figure.
25He uses here Proposition I.45. Notice that he chooses the angle that determines the parallelogram to be a right angle, so that the parallelogram is in fact a rectangle. This is important to the rest of the proof.
26One of the most elementary construction problems, which he solves in Proposition I.10, is to bisect a line segment.
27Here Euclid is citing Proposition II.5, which we will interpret in algebraic terms here to make faster work of his argument, despite the glaring anachronism. Let a = BE and b = EF. Then since BF = a + b, GF = [1/2](a+b), and we have that
|
Now it is straightforward to verify algebraically that
|
and when we rewrite this in terms of the lines in this diagram, we get the result that BE ·EF + EG2 = GF2, which is the algebraic form of the statement that Euclid is asserting here, "the rectangle BE by EF" being given by multiplying its length by its width, and the squares EG and GF being obtained by squaring their sides.
28Of course, he is citing the Pythagorean Theorem (Proposition I.47) here!
29At this point in the argument, Euclid has shown how to square a rectangle. The algebraic form of this result is a significant one: given an x ×y rectangle, the square with side s of equal area satisfies the relation s2 = xy, or equivalently, [(x)/(s)] = [(s)/(y)], so resolving the quadrature of the rectangle is equivalent to finding the square with side \(s=\sqrt{xy}.\) In the diagram (Figure 6), x = EF, y = BE, and s = HE, and since HE is necessarily intermediate in length between EF and BE, it follows that s is between x and y in value. For this reason \(s=\sqrt{xy}\) is also known as the geometric mean between x and y.
Daniel E. Otero (Xavier University), "The Quadrature of the Circle and Hippocrates' Lunes - The Quadrature of Polygons in Euclid's [i]Elements,[/i] Books I, II," Convergence (July 2010)