- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - Trigonometry in the Basic Modern Model
Trigonometry enters into the basic modern model in essentially the same way as the ancient one. This is because the two models are “equivalent”: given a particular planet, the ancient epicycle-deferent model for the planet’s motion gives the same longitudes as the modern model based on a moving earth.
Figure 10 demonstrates the equivalence for an outer planet. (To see things more clearly, start your exploration of this figure by hiding the triangles.)
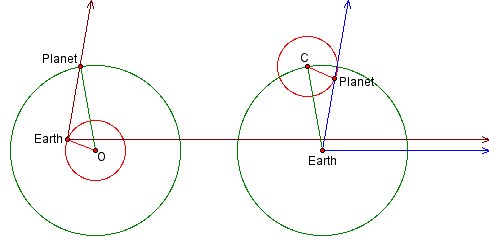
In each model the longitude of the planet is given by the rotating angle centered at the earth; the sides of the angle are brown in the modern model on the left and blue in the ancient model on the right. In both cases one side of the angle points in a fixed direction from the earth, while the other side passes through the planet. In the modern model the earth moves in a circle, bringing the vertex of the angle with it; in the ancient model the earth and the vertex remain stationary. When set in motion, the corresponding sides of the angles remain parallel to each other; thus the longitude is the same under both models. Superimposing the two models, we see that the motion of the planet around its epicycle reflects the earth’s actual motion, while the motion of the center around the deferent reflects the planet’s actual motion.
Figure 11 demonstrates the equivalence for an inner planet. Note that here the role of the epicycle and the deferent are reversed: the epicycle reflects the planet’s actual orbit of the sun, while the deferent reflects the earth’s.
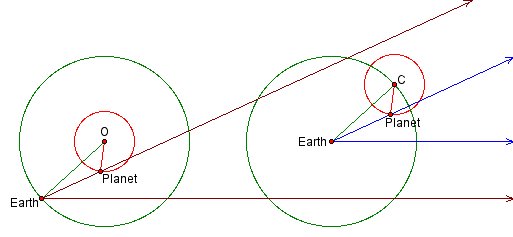
Showing the triangles in the two figures, we can gain some insight into how this equivalence affects computations within the basic modern model. In the ancient model, known information about the motion of the planet around its epicycle and the point C around the deferent translates into information about the triangle formed by the earth, the planet, and the epicycle center C; trigonometry then allows one to calculate parameters and planetary positions. In the modern model, the mathematical situation is virtually unchanged. Known information about the motions of the earth and planet around their circles translates into information about the triangle formed by the earth, the planet, and the center of the earth’s orbit O; parameters and planetary positions are then calculated by solving this triangle. In each case the crucial step is the ability to solve a triangle, a step that is impossible without trigonometry.
Sandra M. Caravella (New Jersey City University), "Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - Trigonometry in the Basic Modern Model," Convergence (August 2010), DOI:10.4169/loci003120




