- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Using Problems from the History of Mathematics - Problems Representing Transitions in Mathematical Thought
Sets of study problems that demonstrate a transition in mathematical thought can be given to students. Mathematical problems from early periods in a society are usually empirically based and task oriented: taxes had to be computed, dikes and walls constructed, grain stored, and the price of merchandise reckoned. Later in the history of the society, one often finds the same problem situations modified to promote mathematical techniques. Thus, in China in 300 B.C.E., surveying concerns prompted the formulation and solution of problems involving towns and landmarks. Typical of such problems is that of a square-walled town. Several measurements outside the walls are given, and the width of the town is desired:
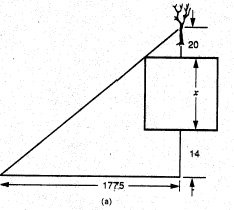
The computational situation gives rise to a quadratic equation where x is the desired width of the town’s wall:
x 2 + 34x - 71000 = 0,
for which the root x = 250 is obtained. By the thirteenth century, such problems had passed out of the realm of surveyors and had become the basis for rather powerful algebraic demonstrations.
An analysis of the Chinese solution processes for the round-wall situation described in the figure below indicates the solution of a tenth-degree equation,
x10 + 15x8 + 72x 6 - 864x 4- 11 664x 2 - 34992 = 0.
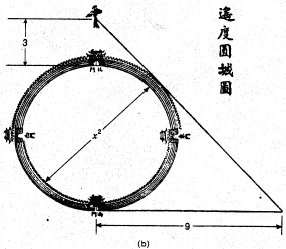
A root of x = 3 was found for the solution. The problem's author, Qin Jiushao, however, was showing off and exhibiting much mathematical bravado. If one lets the diameter of the town be x instead of x2, a much simpler equation for the problem can be found:
x 4 + 6x3 + 9x2 - 972x - 2916 = 0.
Similar situations also abound in European mathematical literature. Problems of partnership were a primary concern in Renaissance Italy of the fifteenth century:
- Three men, Tomasso, Domengo and Nicolo, entered into partnership. Tommaso put in 760 ducats on the first day of January, 1472, and on the first day of April took out 200 ducats. Domengo put in 616 ducats on the first day of February, 1472, and on the first day of June took out 96 ducats. Nicolo put in 892 ducats on the first day of February, 1472, and on the first day of March took out 252 ducats. On the first day of January, 1475, they found that they had gained 3168 ducats, 13 grossi and 1/2. Required the share of each, so that no one shall be cheated. (1 ducat = 24 grossi) [Answer: Tomasso, 1061 ducats, lg; Domengo 949 ducats, 19 1/2 g; Nicolo 1157 ducats, 17g]
This problem can be solved by the use of simple proportions, but a century later partnership problems served as a basis for complex algebraic computation:
- Four men form an organization. The first deposits a given quantity of aurei; the second deposits the fourth power of one-tenth of the first; the third, five times the square of one-tenth the first; and the fourth, 5. Let the sum of the first and second equal the sum of the third and fourth. How much did each deposit? [Answer: 7.4907, 0.3148, 2.8055, and 5, respectively]
Of course problems with historical allure can be assigned merely to demonstrate the mathematical capabilities and skill of our predecessors. A Susa tablet of 2000 B.C.E. requires the reader to find the radius of a circle in which is inscribed an isosceles triangle of sides 50, 50, and 60. An Egyptian counterpart of 150 C.E. asks the reader to find the area of a circle that circumscribes an equilateral triangle whose side is 12 units:
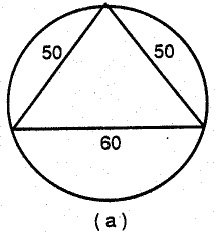
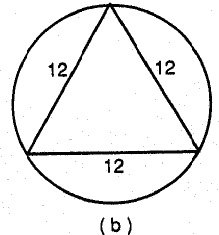
In its Babylonian context, this problem is solved by computing the length of the altitude drawn to the 60-unit side. (The length of the altitude is 40 units.) Radii, r , are then visualized extending to the three vertices of the triangle, and the relationship is established:
r 2 = 302 + (40 - r)2.
Radius r is found to be 31.25 units. The scribe solving the second-century Egyptian counterpart to this problem first used the Pythagorean proposition to find the altitude of the triangle, √108 units, and then applied this result to obtain the area of the triangle, 6√108 square units. Next, he employed a trapezoidal approximation for the area of the remaining circular segment. Multiplying the obtained area by 3, since three congruent segments were involved, he added the result to the triangle's area to obtain a total area for the circle. It appears that the Egyptian calculations were performed using the Babylonian sexagesimal system and the resulting sexagesimal fractions converted into the Egyptian format of sums of unit fractions. The scribe's computation resulted in an answer of 143 + 1/10 + 1/20. How accurate is this result? Is the scribe’s confidence in the trapezoidal approximation for a circular segment well founded?
Frank Swetz (The Pennsylvania State University), "Using Problems from the History of Mathematics - Problems Representing Transitions in Mathematical Thought," Convergence (June 2010), DOI:10.4169/loci002055




