- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Van Schooten's Ruler Constructions - Fourth Solution to Problem I
We repeat Problem I, trisecting a given angle.
Problem I. Given a rectilinear angle BAC, to cut it into two equal pieces.
Van Schooten wrote a fourth solution.
Again another way: Assume in AB the given point G, and from A is located in AC a line AF equal to AB; CA is produced to E so that EA is either larger or smaller than AB. Then produce BA from the point A and place a straight line AD equal to AE; and make through the points E, B and D, F straight lines EBG and DFG, which intersect at G. This done, if the straight line is drawn through AG, it will bisect that angle BAC.
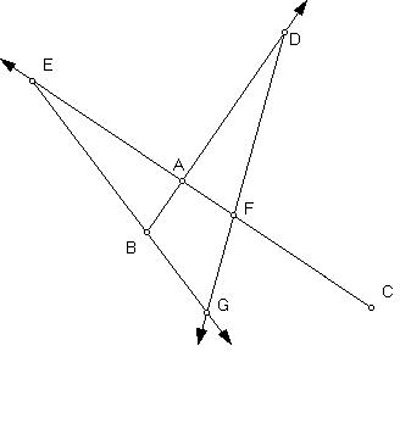
Van Schooten gives two diagrams, depending on whether EA is larger or smaller than AB. We give here the illustration taking EA larger than AB.
Next:
C. Edward Sandifer, "Van Schooten's Ruler Constructions - Fourth Solution to Problem I," Convergence (August 2010)




