- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
A Framework for Technology-Rich Explorations - Illustration of the Framework 1
To better describe and elaborate the proposed framework, we examine the TTP from each of the four levels described in Figure 2 .
Level 1: Data Analysis
First, we provide each of our students with a worksheet that models a specific instance of the ''Two Towers'' scenario (e.g., with PQ = 4 cm and QS= 12 cm). Next, we ask our students to draw a point R anywhere along segment QS then estimate total rope length (i.e. PR+RT) using a centimeter ruler. We show a sample worksheet, annotated with student work, in Figure 3.
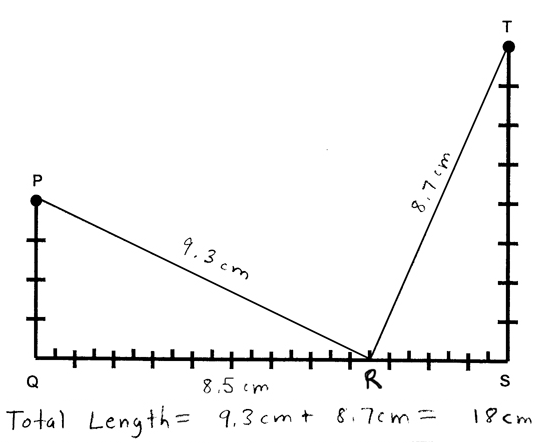
Figure 3. Worksheet modeling the ''Two Towers'' scenario showing student work
After our students successfully complete these initial measurement tasks, we examine their combined data as a whole class. We encourage our students to study the data closely, sharing any observations or hypotheses they may have. Figure 4 illustrates ''Two Towers'' data generated by 22 introductory algebra students. An examination of the data appears to indicate that rope length is minimized when QR=4.0 cm.
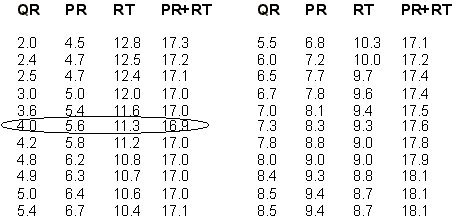
Figure 4. ''Two Towers'' data collected from 22 introductory algebra students
As Figure 4 suggests, students engaged in the initial data collection activity may correctly hypothesize that the length of rope is minimized when line segments QR and PQ are congruent, i.e., when triangle PQR is isosceles. They may also notice that, when this is the case, line segments TR and SQ are also congruent, so triangle TSR is also isosceles -- and therefore triangles PQR and TSR are similar. However, conclusive proof of these conjectures requires more formal mathematics.
Antonio Quesada and Michael Todd Edwards, "A Framework for Technology-Rich Explorations - Illustration of the Framework 1," Convergence (July 2005)




