- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
An Interactive Use of the Lanchester Combat Model - Approximating the Model
When applied to a large but finite number of steps, difference equations can closely approximate the continuous behavior of differential equations. In fact, the continuous model can be seen as a limit of the discrete model. To illustrate this point, we consider the generic Euler discrete approximation method, derived by letting a difference quotient approximate the derivative:
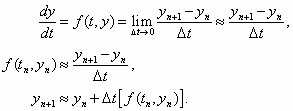
In discrete terms, it is easy to measure the changes occurring on the battlefield by comparing the numbers of troops of each force at different time periods. If we take equal time steps  , and then use this common time step as the unit of time (so
, and then use this common time step as the unit of time (so 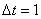 ), we have
), we have
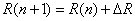 ,
,  .
.
So the future number of one force’s troops equals its current number of troops plus the change in the number of troops, where the change is resulting from battle and non-battle losses and reinforcements. With
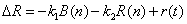 and
and 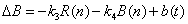 ,
,
the continuous model may be approximated by
 ;
;
 .
.
Captain Bart D. Stewart, "An Interactive Use of the Lanchester Combat Model - Approximating the Model," Convergence (December 2004)




