- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
An Interactive Use of the Lanchester Combat Model - The Lanchester Combat Model
Since it was first proposed during World War I, the Lanchester Combat Model (Lanchester, 1916, Giordano, et al., 1997) in various forms has been used to address quantitatively the competition between opposing forces. The model not only provides insight as to who the victor may be, but it can also approximate how much of each force remains, how long the competing forces remain engaged, and how the changing conditions of battle can impact the outcome.
Consider two opposing forces – Red Force and Blue Force – with respective numbers of troops R(t) and B(t) at time t. Although time is often measured in hours or days, any time frame would suffice. Over time, the numbers of troops available for combat change for various reasons – perhaps the most important being combat losses.
Combat losses are indicative of the ability of one force to eradicate the other. When conventional forces meet, combat losses are considered to occur at a rate proportional to the number of troops of the opposing force. Assuming that the Blue Force and Red Force can inflict combat losses on each other at proportional rates of k1 and k3, respectively, we can model the changes in their troop numbers by
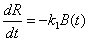 ,
,  .
.
While combat losses account for much of the change on the battlefield, non-combat losses can further degrade troop availability. We assume that the forces sustain these losses at rates proportional to their own numbers. Thus, if the proportionality constants are k2 for the Red Force and k4 for the Blue Force, the model becomes
 ,
,  .
.
The final component of this model is troop reinforcement. With the Red Force and Blue Force getting reinforcements at rates of r(t) and b(t), respectively, the combat model with initial conditions becomes
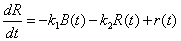 ,
, 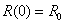 ;
;
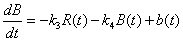 ,
, 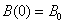 .
.
Captain Bart D. Stewart, "An Interactive Use of the Lanchester Combat Model - The Lanchester Combat Model," Convergence (December 2004)




