- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Exploration: Exponential Functions and Derivatives - Calculating the Derivative
To compute the derivative of the function f(x)=ex, use the definition of the derivative as a limit of a difference quotient:
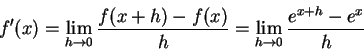
This limit can be simplified using properties of exponents:

Now, in the numerator, factor out the common ex:
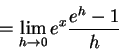
Since the limit is with respect to the variable h, and the variable x is independent of h, the ex may be treated as a constant factor and removed completely from the limit:
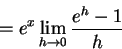
The remaining limit (not including the ex factor) is the critical limit for finding the derivative of f(x)=ex -- if this limit exists and is equal to K, then f '(x)=K ex. It remains only to find K (if it exists). For the purposes of plugging into the applet below to find K, rewrite the limit in terms of the variable x instead of h:
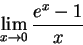
Now use the tables in the applet below to approximate the value of K.
From these tables, it seems that K=1. This is an approximation to K using the values in the tables from the applet, but it seems to be a good approximation, given the trends in the tables. If this is the case, then (from above)
This formula is important enough to bear repeating:
Tom Leathrum, "Exploration: Exponential Functions and Derivatives - Calculating the Derivative," Convergence (October 2004)




