- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Logistic Growth Model - Summary
- Explain in your own words the difference(s) between an exponential growth model and a logistic growth model.
- The U.S. Census data from 1790 through 1940 was roughly logistic. What happened after that to interrupt this pattern?
- Explain in your own words the meanings of the parameters r and K in the logistic differential equation
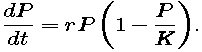
- Sometimes the graph of the solution of a logistic equation has an inflection point. How is the location of this inflection point related to K? What is the significance of the inflection point in terms of population growth rate?
- Suppose a population has a logistic growth rate and the starting population is greater than the carrying capacity. What would you predict about the future of the population? Why?
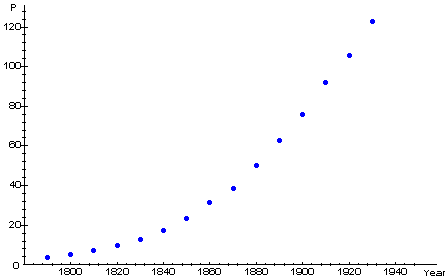
- In our second attempt at fitting parameters to the U.S. population data (Part 7), we had the advantage of starting with a good estimate of K, the maximum supportable population -- but only because we did the fit in Part 6 first. Suppose you had only a plot of the data, as in the figure below. How would you estimate K from this plot? Would your estimate be close to the final value of K you chose in Part 7? Explain.
Leonard Lipkin and David Smith, "Logistic Growth Model - Summary," Convergence (December 2004)




