- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Raindrops - Falling Bodies with Air Resistance
We now investigate a more sophisticated model for a falling body, one that takes into account the resisting force of the air through which the object falls. The usual physical assumption is that the force of air resistance is proportional to some power of the velocity, but the particular power (first, second, or other) depends on the particular object.
We consider raindrops falling from a cloud 3000 feet above the ground. If the raindrop is small, say a drop of diameter 0.003 inches (or 0.00025 feet), a size found in a drizzle, the force of air resistance is modeled well by a multiple of the first power of the velocity. In other words, the resisting force can be described by

for some positive constant k. (The minus sign indicates that the force is in the direction opposite to the velocity, i.e., upward.) When combined with the force of gravity,

this yields the total force on the raindrop:

We recall Newton's Second Law of Motion:
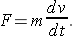
Equating our two formulas for the force F and dividing by m, we find a new differential equation for velocity:

We'll let c represent the quotient k/m. When we attach our initial condition, v(0) = 0, we obtain our new initial value problem:

Experimental evidence gives an approximate value of 52.6 sec-1 for c, when distances are in feet and the drops are drizzle size.
- Why must the unit for c be sec-1 (reciprocal seconds)?
- Enter the new formula for the derivative dv/dt in your worksheet, and construct a slope field for this formula. (Note that the time and velocity scales provided in the worksheet are very different from those on Page 2.)
- Using the slope field as a guide, make a guess as to what type of function might be a solution to this differential equation, and enter your guess in the worksheet. (If you know how to solve the equation exactly, enter the actual solution.) Does your proposed solution satisfy the initial condition?
- Plot your proposed solution -- either in your worksheet or on your calculator -- to see if you are on the right track. Does your proposed solution have the right shape to fit the direction field? Why or why not? (Note: There is no plot command for this in the worksheet, but you can enter a command on your own. Don't worry at this point if you can't find or don't know a symbolic solution -- the rest of the module is about an alternative to such solutions.)
Guessing a formula for v as a function of time may be more difficult for this problem than actual calculation was on Page 2. You may or may not know a systematic way to solve this type of problem at this point. On the next page we will take a different approach and use a numerical technique called Euler's Method. This technique will only approximate the desired solution, but it has the distinct advantage of applicability to any initial value problem.
David A. Smith and Lawrence C. Moore, "Raindrops - Falling Bodies with Air Resistance," Convergence (December 2004)




