- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Special Relativity and Conic Sections - Interpretation of the Experiment
![]() Mathwright Microworld for this page
Mathwright Microworld for this page
PDF version of this page
|
In order to understand what the experiment means, we must write down the equation of the curve defined by projecting the wavefront curve at ![]() to the (standard) coordinates of the
to the (standard) coordinates of the ![]() plane of
plane of ![]() . I do this by introducing certain coordinates for the
. I do this by introducing certain coordinates for the ![]() plane of
plane of ![]() . (We saw this in a Euclidean context in Note 3 of Planes Intersecting Cones.) The "speed" of
. (We saw this in a Euclidean context in Note 3 of Planes Intersecting Cones.) The "speed" of ![]() (as measured by
(as measured by ![]() ) is defined to be
) is defined to be
|
|
I assume for this experiment that ![]() -- otherwise, there is nothing to do.
-- otherwise, there is nothing to do.
We saw that the wavefront curve was an ellipse in the (stationary) frame of ![]() by using the basis
by using the basis ![]() in
in ![]() coordinates, given by
coordinates, given by
![]() ,
,
![]() ,
,
![]() ,
,
where these vectors satisfy the hyperbolic orthogonality relations,
|
|
Note 10. Coordinates adapted to the projected ellipse
We see that there are orthogonal unit vectors U and V in the ![]() plane of
plane of ![]() so that the projected ellipse is given by the parametric equation
so that the projected ellipse is given by the parametric equation
|
|
(9.1) |
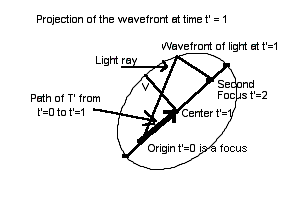 From this it follows that the projected curve is an ellipse with major axis on the line generated by
From this it follows that the projected curve is an ellipse with major axis on the line generated by ![]() , as illustrated at the right.
, as illustrated at the right.
Here is the interpretation: The projected ellipse is the projection to the ![]() plane of the
plane of the ![]() observer of his measured spatial positions of the wavefront at the
observer of his measured spatial positions of the wavefront at the ![]() observer's time
observer's time ![]() . It is not a circle because this wavefront does not consist of simultaneous events for
. It is not a circle because this wavefront does not consist of simultaneous events for ![]() (since
(since ![]() ).
).
The major axis of this ellipse contains, between the focus at the origin and the second focus, the line of spatial positions of the world-line of ![]() between his time
between his time ![]() . In particular, he moves from the origin (first focus) to the center in 1 unit of his time, which is
. In particular, he moves from the origin (first focus) to the center in 1 unit of his time, which is ![]() units of the
units of the ![]() observer's time. His projection must therefore move to the second focus at his time
observer's time. His projection must therefore move to the second focus at his time ![]() .
.
The rays of light, emitted at various angles from the emission event, project to segments connecting the first to the second focus via a point on the boundary of the projected ellipse. The questions, of course, are:
-
Why should the sum of the lengths be constant?
-
What does this constant sum represent?
And the answers will now be fairly easy to see.
Consider a ray of light that bounces from the emission to the reception event. Describe its itinerary in the reference frame of observer ![]() . It starts from the origin event
. It starts from the origin event
|
|
and arrives at the mirror at event
|
|
Next, it reflects to the reception event,
|
|
In the first leg of its itinerary, it lies in the light cone, so
|
|
Since the square roots of both sides of this equation are equal, we conclude that the spatial ![]() projection of that path has length
projection of that path has length ![]() , which is
, which is ![]() , since
, since ![]() .
.
In the second leg of its itinerary, it also lies in a light cone, so
|
|
For the same reason, the spatial projection of that path has length ![]() .
.
Therefore, the sum of the spatial lengths is ![]() . This is equal to the time that observer
. This is equal to the time that observer ![]() measures from the emission event to the reception event. That is, of course, the time coordinate in the frame of
measures from the emission event to the reception event. That is, of course, the time coordinate in the frame of ![]() of the event
of the event ![]() . But from the definition of
. But from the definition of ![]() in the previous section,
in the previous section,
|
|
we see that this is
|
|
And this, of course, is the length of the major axis of the projected ellipse. That is a physical interpretation of why the sum of the lengths of the paths from a point on the ellipse to its foci is constant. It is the time ![]() measures between the emission and reception event, which is the same for all rays of light.
measures between the emission and reception event, which is the same for all rays of light.
Next, I consider the focus-directrix property of the ellipse. I showed in Planes Intersecting Cones that the intersection of the plane of simultaneity ![]() for
for ![]() with the plane of simultaneity
with the plane of simultaneity ![]() for
for ![]() is a line that I call
is a line that I call ![]() :
:
![]() .
.
I represented the tangent plane, the plane of simultaneity ![]() for
for ![]() , as the graph of a function of x and y:
, as the graph of a function of x and y:
|
|
In the present context, the function ![]() has the following interpretation. With each point
has the following interpretation. With each point ![]() there is a unique point on the plane of simultaneity
there is a unique point on the plane of simultaneity ![]() for
for ![]() that projects to it.
that projects to it. ![]() is the time coordinate that standard observer
is the time coordinate that standard observer ![]() ascribes to it. The line
ascribes to it. The line ![]() is the set of events with
is the set of events with ![]() and
and ![]() .
.
Note 11. Interpretation of the eccentricity
The calculation above shows that the value of the eccentricity ![]() is the speed of
is the speed of ![]() as measured by
as measured by ![]() ,
,
![]() =
= ![]() ,
,
and it gives us the focus-directrix property of the projected ellipse.
Now, we might ask how general this construction is. It is clear that, for any particular direction of motion of ![]() with respect to
with respect to ![]() , we will obtain among the projected ellipses one representative of the similarity class of ellipses for each speed
, we will obtain among the projected ellipses one representative of the similarity class of ellipses for each speed ![]() . And every similarity class will be represented, simply by choosing the representative with semi-minor axis of length 1, and semi-major axis of length
. And every similarity class will be represented, simply by choosing the representative with semi-minor axis of length 1, and semi-major axis of length
|
|
Therefore this physical argument is completely general.
What happens if ![]() is stationary with respect to
is stationary with respect to ![]()
![]() ? In that case, this construction breaks down when we attempt to build the
? In that case, this construction breaks down when we attempt to build the ![]() observer's orthonormal basis. But in that case, there is no need to build such a basis. The foci collapse to the center, the ellipse is a circle, and everything happens as it does in the frame of
observer's orthonormal basis. But in that case, there is no need to build such a basis. The foci collapse to the center, the ellipse is a circle, and everything happens as it does in the frame of ![]() .
.
James E. White, "Special Relativity and Conic Sections - Interpretation of the Experiment," Convergence (October 2004)




