- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Equiangular Spiral - Background: Spirals in Nature
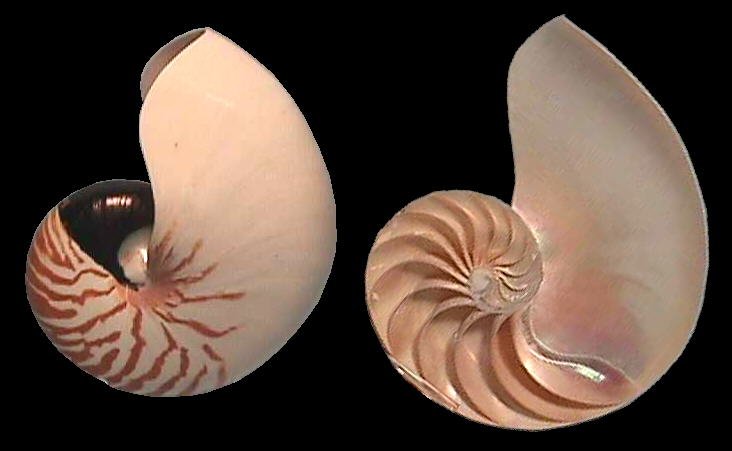
In this module you will discover some of the properties of a fascinating curve, the equiangular spiral, which abounds in nature. The spiral forms of many shells, fossils, horns, nails, and hairs closely resemble this curve. Our investigation will focus on one of the most elegant of these examples, the shell of the chambered nautilus (Nautilus pompilius). Here is a picture* of a nautilus shell, together with a cross-section that shows the chambers from which it gets its name.
Why should the equiangular spiral be so prevalent in nature?
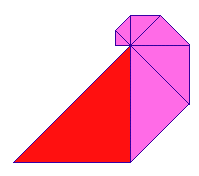 Aristotle, writing in about 350 BCE, noticed that certain biological forms grow by adding units that are always the same shape, differing only in magnitude. Such shapes are called gnomons, and the study of "gnomonic growth" occupied a large part of Greek mathematics. We illustrate this idea with a growing spiral of isosceles right triangles, in which each new triangle has a leg that coincides with the hypotenuse of the preceding triangle. The most recent addition (shaded red) is a gnomon to the rest of the figure. Even in this very crude model we see a spiral pattern emerging.
Aristotle, writing in about 350 BCE, noticed that certain biological forms grow by adding units that are always the same shape, differing only in magnitude. Such shapes are called gnomons, and the study of "gnomonic growth" occupied a large part of Greek mathematics. We illustrate this idea with a growing spiral of isosceles right triangles, in which each new triangle has a leg that coincides with the hypotenuse of the preceding triangle. The most recent addition (shaded red) is a gnomon to the rest of the figure. Even in this very crude model we see a spiral pattern emerging.
The British naturalist D'Arcy Thompson (On Growth and Form, 1917) observed gnomonic growth in many natural forms: "It is characteristic of the growth of the horn, of the shell, and of all other organic forms in which an equiangular spiral can be recognized, that each successive increment of growth is similar, and similarly magnified, and similarly situated to its predecessor, and is in consequence a gnomon to the entire pre-existing structure."
Here are some links to other sites at which you can pursue ideas related to gnomonic growth and equiangular spirals:
- Time and Tide, Spira Solaris, spiral nebulae, and Fibonacci numbers in astronomy
- Fibonacci Numbers and Nature, spiral patterns in leaves and seeds
- Equiangular Spiral, history, associated curves, Java applet
* Picture contributed by Bret Raines of The Molluscs Net (link is no longer available).
Lang Moore, David Smith, and Bill Mueller, "The Equiangular Spiral - Background: Spirals in Nature," Convergence (December 2004)




