- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Linear Algebra Behind Search Engines - An Advanced Vector Space Model: LSI
The vector space model provides the framework for most information retrieval algorithms used today. However, this most basic vector space model alone is not efficient enough. Many modifications and heuristics have been invented to speed up the basic model, giving rise to a popular model called the Latent Semantic Indexing (LSI) model (Berry, Drmac & Jessup, 1999).
The major mathematical entity in the LSI model is also a matrix. We have already discussed how the vector space model described in preceding pages can be viewed as a matrix. Now let's adjoin the 3 billion document vectors associated with the Web (each of which is a 300,000-D vector) to one another to form a 300,000-by-3,000,000,000 matrix, which is called the term-by-document matrix. This matrix might look like

where the (i,j)-element of the matrix contains a 1 if the word for position i in document j is a keyword and a 0 otherwise. Column 1 in this matrix is document 1's document vector, column 2 is document 2's vector, and so forth.
This huge term-by-document matrix may contain redundant information. Berry, Drmac & Jessup (1999) provide the following example:
There may be a document on the Web with keywords applied linear algebra and another document on the Web with keywords computer graphics. There might also be a document with keywords linear algebra applied [to] computer graphics. Clearly, the vectors for the first two documents sum to the vector for the third document.
In linear algebra, this is called dependence among columns of the matrix. This dependence among columns may be frequent, since there are so many documents on the Web. Fortunately, this dependence in the term-by-document matrix can be used to reduce the work required in information retrieval.
Here is where the LSI model departs from the vector space model. In most general terms, the LSI method manipulates the matrix to eradicate dependencies and thus consider only the independent, smaller part of this large term-by-document matrix. In particular, the mathematical tool used to achieve the reduction is the truncated singular value decomposition (SVD) of the matrix.
Note: We introduce the SVD briefly in what follows; Berry, Drmac & Jessup (1999) and Meyer (2000) contain detailed explanations of the SVD of a matrix.
Basically, a truncated SVD of the term-by-document matrix reduces the m-by-n matrix A to an approximation Ak that is stored compactly with a smaller number of vectors. The subscript k represents how much of the original matrix A we wish to preserve. A large value of k means that Ak is very close to A. However, the value of this good approximation must be weighed against the desire for data compression. In fact, the truncated representation Ak requires the storage of exactly k scalars, k m-dimensional vectors and k n-dimensional vectors. Clearly, as k increases, so do the storage requirements.
Let's pause now for a formal definition of the SVD, followed by a numerical example. Before defining the SVD, we also review some other matrix algebra terms. The following definitions and theorems are taken from Meyer (2000).
Definition The rank of an m-by-n matrix A is the number of linearly independent rows or columns of A.
Definition An orthogonal matrix is a real m-by-n matrix P of rank r whose columns (or rows) constitute an orthonormal basis for Rr. That is, the set of column (or row) vectors {p1, p2, …, pr}, where r = rank(P), has the property that piTpj = 1 for i = j, 0 otherwise.
Theorem For each m-by-n matrix A of rank r, there are orthogonal matricesUm-by-m and Vn-by-n
and a diagonal matrix
Dr-by-r = diag(σ1, σ2, …, σr)
such that
with σ1 ≥ σ2 ≥ … ≥ σr > 0.
Definition The σi's in the preceding theorem are called the nonzero singular values of A. When r < p = min(m,n), A is said to have p - r additional zero singular values. The factorization in the theorem is called the singular value decomposition (SVD) of A, and the columns of U (denoted ui) and the columns of V (denoted vi) are called the left-hand and right-hand singular vectors of A, respectively. Written another way, the SVD expresses A as a sum of rank-1 matrices:
.
Definition The truncated SVD is
Theorem (Meyer, 2000, p. 417) If σ1 ≥ σ2 ≥ … ≥ σr are the nonzero singular values of Am-by-n, then for each k, the distance from A to the closest rank-k matrix is
Thus, σk+1 is a measure of how well Ak approximates A. In fact, for Am-by-n of rank r, Ak is the best rank-k matrix approximation to A (Eckart & Young, 1936). The goal in using Ak to approximate A is to choose k large enough to give a good approximation to A, yet small enough so that k << r requires much less storage.
Figure 6 shows the storage savings obtained with the truncated SVD in general.

Figure 6: Data compression using truncated SVD
A numerical example may make these concepts clearer. Suppose the original term-by-document matrix A is 100-by-300. After a truncated SVD, suppose A20 approximates A well, i.e., we take k = 20. To calculate the storage savings, we count the number of elements that must be stored in both representations -- the full 100-by-300 matrix A (30,000 elements) versus the truncated SVD representation, which requires storage of a 20-by-1 vector, a 100-by-20 matrix and a 20-by-300 matrix (20 × 1 + 100 × 20 + 20 × 300 = 8,020 elements). The number of elements in the full matrix A representation is almost 4 times greater than the number of elements required by the truncated SVD.
Larger data collections often have much greater storage savings. The Medlars collection uses a 5831 × 1033 term-by-document matrix, which can be very well approximated by the truncated SVD with k = 70, creating storage savings about 13 times less than the original matrix.
We close this section with a small example, taken from Berry & Browne (1999), showing that the truncated SVD can well approximate a matrix. Suppose A is the 9 × 7 matrix
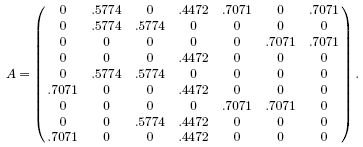


Table 3: Cosines of angles between document vectors and query using A and A3
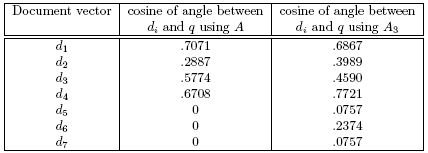
As k increases, the truncated SVD better captures the essence of A, yet the storage savings decrease. For example, here is A6:

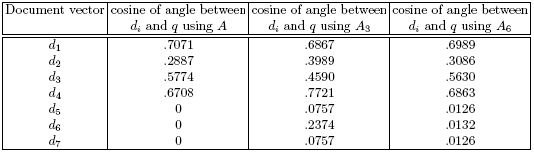
Notice that A6 does a much better job of capturing the relationship between the vectors of A than A3 does. Now compare the ranking of document vectors using A with the ranking obtained using A6. Also compare the ranking from A3 with that from A6.
Table 4: Absolute cosines of angles between document
vectors and query using A, A3, and A6
Having demonstrated the truncated SVD's potential to save storage (note), let's now consider how the angle measures are computed using Uk, Dk, Vk. Recall the formula for computing the cosine of the angle &thetai between document vector di and query vector q:
![]()
![]()
![]()
![]()

since ||UksiT||2= ||siT||2 for the orthogonal matrix Uk, and ||siT||2=||si||2.
It's helpful to review the above equation, emphasizing the advantages of the truncated SVD. First, Uk, si and ||si||2 only need to be computed once and can be reused for each query q. At runtime, only UkTq and ||q||2 must be computed. The vectors in Uk and Vk are computed once, and these can be determined without computing the entire SVD of A, since there is an algorithm for computing the first k singular values and vectors iteratively (Golub & Van Loan, 1996).
In practice, k can be much smaller than r and yet Ak still approximates A well. One reason for this concerns the noise in A due to polysemous and synonymous words in the English language. Truncating the SVD reduces this noise. Another reason why k << r works well in information retrieval applications is that numerical accuracy is of little concern. For example, three digits of precision in the cosine measure may be sufficient. That is, a cosine measure of .231 is just as meaningful as the more numerically precise result of .23157824. The truncated SVD enables storage benefits and still maintains adequate accuracy in the angle measure calculations.
Exercise: Experiment with an LSI Search Engine built in Matlab
Amy Langville, "The Linear Algebra Behind Search Engines - An Advanced Vector Space Model: LSI," Convergence (December 2005)





