- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Linear Algebra Behind Search Engines - Focus on the Vector Space Model
Of the basic models of information retrieval, we focus in this project on the Vector Space Model (VSM) because it has the strongest connection to linear algebra. This model and its more advanced version, Latent Semantic Indexing (LSI), are beautiful examples of linear algebra in practice.
Let's begin with a trivial example. Consider the database of articles for a hypothetical periodical called Food! magazine. The articles are distinguishable by only three keywords: desserts, breads, vegetables. One article (document 1) talks only about desserts. Another article (document 2) discusses only breads. A third article (document 3) is 30% about vegetables and 70% about breads. All divisions of article space among the three keywords are possible. Vectors and matrices are used to describe how a vector space search engine processes a query in the Food! database.To store data about the division of topics discussed in the particular Food! document number 1, we use the column vector
 All of the document vector information can be stored together in a matrix. Suppose there are only 7 documents labeled d1, d2, d3, d4, d5, d6, d7, in the Food! database and only the three keywords (desserts, breads, vegetables) to distinguish article topics. Then, the matrix A capturing the data for Food! documents is
All of the document vector information can be stored together in a matrix. Suppose there are only 7 documents labeled d1, d2, d3, d4, d5, d6, d7, in the Food! database and only the three keywords (desserts, breads, vegetables) to distinguish article topics. Then, the matrix A capturing the data for Food! documents is

Note: There are numerous matrix element weighting schemes for VSM methods. Here we are using the proportion of the document dealing with each corresponding term, but various other weights, such as the frequency of a term's usage in a document, could be used (Jones & Furnas, 1987).
A is a 3-by-7 matrix. If there were, say, 20 keywords and 1000 documents, then A would be a 20-by-1000 matrix. A is called a term-by-document matrix because the rows correspond to terms (keywords) in the database and the columns correspond to documents. Since there are only three terms in our Food! example, we can plot each column (document) vector in the matrix A in three-dimensional space. A static plot of the seven document vectors is shown in Figure 1 -- to see an animated version, click on the figure. When you are ready to return here, close the animation window.
Figure 1. 3-D plot of 7 document vectors
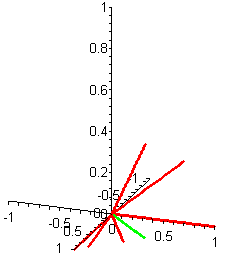
Let's analyze this plot to see if it gives us any insight into the information retrieval problem of searching the Food! database to find the document closest to a given query. Suppose a user of this Food! search engine wants to find all articles related to a query of vegetables. Then our query vector is  Now the problem is mathematical: Find which documents represented by the vectors (d1, d2, d3, d4, d5, d6, d7) are "closest" to this query vector q. You might try to inspect the 3-D plot of the document vectors and the query vector visually (Figure 2) to see which document vectors are "closest." This visual inspection can be difficult, since the display of a 3-D plot must be done on a 2-D screen -- but, as with Figure 1, you can click on the figure to see an animated version. Can you guess which document vectors are closest to the query vector? Why did you make that choice?
Now the problem is mathematical: Find which documents represented by the vectors (d1, d2, d3, d4, d5, d6, d7) are "closest" to this query vector q. You might try to inspect the 3-D plot of the document vectors and the query vector visually (Figure 2) to see which document vectors are "closest." This visual inspection can be difficult, since the display of a 3-D plot must be done on a 2-D screen -- but, as with Figure 1, you can click on the figure to see an animated version. Can you guess which document vectors are closest to the query vector? Why did you make that choice?
Figure 2. 3-D plot of 7 document vectors (red) and query vector (green)
The information contained in a multi-dimensional vector can be summarized in two one-dimensional measures, length and angle with respect to a fixed direction. The length of a vector is the distance from the tail to the head of the vector. The angle between two vectors is the measure (in degrees or radians) of the angle between those two vectors in the plane that they determine. Keeping the length and angle (relative to the query vector) of the Food! vectors in mind, try to answer this question:
Visually, what is it about document 4's vector that makes it most similar to the query vector?
Clearly, it is not the length of the vector -- document 1's vector has the same length as the query vector, but it does not appear to be physically "closest" to the query vector. Rather, the angle of the vector with the query vector tells us that document 4's vector is closest to the query vector. For each document in the Food! database, we can use one number, the angle between the document vector and the query vector, to capture the physical "distance" of that document from the query. The document vector whose direction is closest to the query vector's direction (i.e., for which the angle is smallest) is the best choice, yielding the document most closely related to the query.
We can compute the cosine of the angle θ between the nonzero vectors x and y by
![]()
![]()
Table 1. Cosines of angles between Food! document vectors and query vector 1
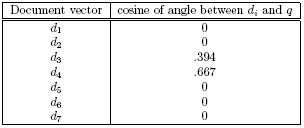
If the cosine of an angle is 1, then the angle between the document vector and the query vector measures 0°, meaning the document vector and the query vector point in the same direction. A cosine measure of 0 means the document is unrelated to the query, i.e., the vectors are perpendicular. Thus, a cosine measure close to 1 means that the document is closely related to the query.
Note: Since all entries in the vectors are nonnegative, the dot products are nonnegative, which means there is no need to take absolute value of the cosine measure.
We now consider a second query, this time desiring articles with an equal mix of information about desserts and breads, so the new query vector is ![]() We show the cosines of the angles between the document vectors and this query vector is in Table 2.
We show the cosines of the angles between the document vectors and this query vector is in Table 2.
Table 2: Cosines of angles between Food! document vectors and query vector 2

We see that document 6 is now most relevant to the query -- as expected, since d6 is identical to query vector 2 in the divisions of topics discussed. Document 5 is the second most relevant document to query 2, followed by document 7.
In practice, a search engine system must designate a cutoff value. Only those documents whose angles with the query vector are above this cutoff value are reported in the list of retrieved documents viewed by the user. In Figure 3 we show (in blue) the cone of all vectors whose angle with the query vector is 45°. The cosine of this angle is 0.7071, and thus, if we want to return only documents whose vectors lie inside (or on) the cone, the cutoff value is 0.7071. (As before, click on the figure to see an animated version.)
Figure 3. Two views of cone around query vector created by cutoff value
If, for example, the cutoff value for query 2 is 0.9, then only d5 and d6 are returned to the user as relevant (see Table 2 again). If, however, a cutoff value of 0.7 is selected, all but d3 will be returned as relevant. Thus, choosing an appropriate cutoff value is not a trivial task and clearly affects both the precision and recall of the search engine.
A quick look at the plot in Figure 4 (or its animated version) of these same document vectors with the query 2 vector shows that d6, d5 and d7 are indeed closest to q in angle measure. Of course, this visual inspection method can be deceptive at times, which is why information retrieval researchers always resort to the nice theoretical underpinnings they have derived as mathematical formulas to compute the cosines of these angles.
Figure 4. 3-D plot of 7 document vectors and query vector 2
Now let's review how the VSM processes query q. First, the cosine of the angle measure between each di and q must be computed. Those distance measures exceeding some predetermined cutoff value are ranked, and the ranked list is presented to the user. For practical collections, much larger than this trivial 3-term-7-document collection, computing these distance measures is the main computational expense.
Exercise: Create Your Own 3-D Physical Search Engine
Amy Langville, "The Linear Algebra Behind Search Engines - Focus on the Vector Space Model," Convergence (December 2005)