- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Method of Characteristics & Conservation Laws - Special Case: \(b(x, t) = 1\) and \(c(x, t) = 0\)
We will examine the method of characteristics for three different PDEs:
For all three examples, the initial conditions are specified as ![]() . The examples take a slightly simpler form than the general equation (1). All three examples have b(x,t) = 1 and c(x,t) = 0. In this case characteristic equation (2b) becomes
. The examples take a slightly simpler form than the general equation (1). All three examples have b(x,t) = 1 and c(x,t) = 0. In this case characteristic equation (2b) becomes ![]() ,.and the solution is t = s+ k. Using the initial condition t(0) = 0, we determine that the constant is k = 0, so s = t. In this special case with b(x,t) = 1, we only have one characteristic equation to solve. Before proceeding to the examples, we restate the general strategy in terms of this special case.
,.and the solution is t = s+ k. Using the initial condition t(0) = 0, we determine that the constant is k = 0, so s = t. In this special case with b(x,t) = 1, we only have one characteristic equation to solve. Before proceeding to the examples, we restate the general strategy in terms of this special case.
-
Step 3. We now have a solution
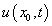 . Solve for
. Solve for  in terms of x and t, using the results of Step 1, and substitute for
in terms of x and t, using the results of Step 1, and substitute for  in
in 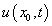 to get the solution to the original PDE as
to get the solution to the original PDE as  .
.
Constant Coefficient Advection Equation
The advection equation is the PDE
![]() , (4)
, (4)
where a is a real constant, the wave speed or velocity of propagation. This is the rate at which the solution will propagate along the characteristics. The velocity is constant, so all points on the solution profile will move at the same speed a.
Now we apply the method of characteristics outlined in the 3 steps above.
-
Step 1. The characteristic equation (2a) to solve is
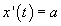 with the initial condition
with the initial condition  . The solution
. The solution 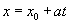 gives the characteristic curves, where
gives the characteristic curves, where  is the point at which each curve intersects the x-axis in the x-t plane.
is the point at which each curve intersects the x-axis in the x-t plane. -
Step 3. The characteristic curves are determined by
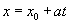 , so
, so 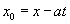 , and the solution of the PDE is
, and the solution of the PDE is 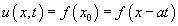 .
.
To verify that ![]() does indeed remain constant along the characteristics, we differentiate
does indeed remain constant along the characteristics, we differentiate ![]() along one of these curves to find the rate of change of u along the characteristic:
along one of these curves to find the rate of change of u along the characteristic:
![]()
So we find that the rate of change is zero, verifying that u is constant along the curve.
By writing the characteristic curves as ![]() , we see that, in the x-t plane, the characteristics are parallel lines with slope 1/a, so the slope of the characteristics depends only on the constant a.
, we see that, in the x-t plane, the characteristics are parallel lines with slope 1/a, so the slope of the characteristics depends only on the constant a.
Experiment in the applet with different values of the wave speed a, which can be changed through the dialog box displayed when the parameters button is pressed. Set ![]() to observe the solution profile moving in the opposite direction, and observe the negative slope of the characteristics.
to observe the solution profile moving in the opposite direction, and observe the negative slope of the characteristics.
Variable Coefficient Advection Equation
The variable coefficient advection equation is
![]() . (5)
. (5)
For this example, we take ![]() , so the wave speed depends on the spatial coordinate x. That is, the speed of a point on the solution profile will depend on the horizontal coordinate x of the point.
, so the wave speed depends on the spatial coordinate x. That is, the speed of a point on the solution profile will depend on the horizontal coordinate x of the point.
-
Step 1. The characteristic equation (2a) is
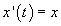 with the initial condition
with the initial condition  . Thus the characteristic curves are
. Thus the characteristic curves are 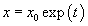 .
. -
Step 3. The characteristic curves are determined by
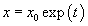 , so
, so 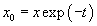 , and the solution of the PDE in the original variables is
, and the solution of the PDE in the original variables is 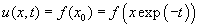 .
.
View the variable coefficient advection equation simulation in the applet. Notice that the characteristics are not straight lines. Also observe that the characteristics do not intersect.
Scott A. Sarra, "The Method of Characteristics & Conservation Laws - Special Case: \(b(x, t) = 1\) and \(c(x, t) = 0\)," Convergence (September 2004)




