- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The SIR Model for Spread of Disease - Relating Model Parameters to Data
The infectious period for Hong Kong Flu is known to average about three days, so our estimate of k = 1/3 is probably not far off. However, our estimate of b was nothing but a guess. Furthermore, a good estimate of the "mixing rate" of the population would surely depend on many characteristics of the population, such as density. In this part, we will experiment with the effects of these parameters on the solutions, and then try to find values that are in agreement with the excess deaths data from New York City. We focus our experimentation on the infected-fraction, i(t), since that function tells us about the progress of the epidemic.
- First let's experiment with changes in b. Keep k fixed at 1/3, and plot the graph of i(t) with several different values of b between 0.5 and 2.0. Describe how these changes affect the graph of i(t). Stay alert for automatic changes in the vertical scale. If you're not sure what is changing, vary your colors and overlay consecutive graphs.
- Explain briefly why the changes you see are reasonable from your intuitive understanding of the epidemic model.
- Now let's experiment with changes in k. Return b to 1/2, and experiment with different values of k between 0.1 and 0.6. Describe the changes you see in the graph of i(t). Again, be alert for automatic changes in the vertical scale. If you're not sure what is changing, vary your colors and overlay consecutive graphs.
- Explain the changes you see in terms of your intuitive understanding of the model.
- There is a change in the character of the graph of i(t) near one end of the suggested range (0.1 to 0.6) for k. What is the change, and where does it occur?
- Use the infected-fraction differential equation
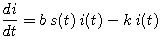
to explain how you could have predicted in advance the value of k at which the character of the graph of i(t) changed. - Now let's compare our model with the data. Recall that these were the numbers of deaths each week that could be attributed to the flu epidemic. If we assume that the fraction of deaths among infected individuals is constant, then the number of deaths per week should be roughly proportional to the number of infecteds in some earlier week. We repeat the graph of the data, along with the graph of i(t) with k = 1/3 and b = 6/10. Does the model seem reasonable or not? Explain your conclusion.
 |
 |
David Smith and Lang Moore, "The SIR Model for Spread of Disease - Relating Model Parameters to Data," Convergence (December 2004)




