- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Three Party Elections: Interactive Examples - Pairwise Elections and the Condorcet Winner
In the late 1700's, the Marquis de Condorcet proposed an alternative to the voting method put forth by Jean-Charles de Borda. Since there can be no confusion as to the winner of a two-way election, Condorcet's idea was to consider all possible pairwise elections among the candidates.
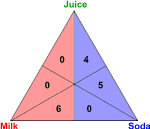
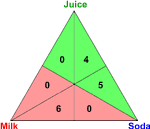
Recall the "milk, soda, juice" example. If we hold an election between just milk and soda, the 6 voters that have milk top-ranked vote for milk and the 5 voters that have soda top-ranked vote for soda. The 4 remaining voters have juice top-ranked, but they can't vote for juice. Instead they have to vote for their second choice, soda. Thus soda wins the milk versus soda election by a score of 9 to 6. The other pairwise elections are shown below.
 |
 |
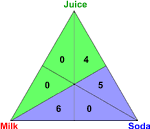 |
| Milk versus Soda | Milk versus Juice | Soda versus Juice |
| Soda wins 9-6 | Juice wins 9-6 | Soda wins 11-4 |
|---|
Notice that, using the representation triangle, it is easy to add up a candidate's score in a pairwise election. Simply divide the triangle in half between the two candidates and add up the numbers on each side.
If one candidate wins all of the pairwise elections he is involved in, we call that candidate the Condorcet winner. If a candidate loses all of the pairwise elections he is involved in, that candidate is the Condorcet loser. In our example, soda wins both of its pairwise elections, so soda is the Condorcet winner. Since milk loses both of its pairwise elections, milk is the Condorcet loser.
Unfortunately, sometimes pairwise elections do not give us a decisive winner. Consider the following profile:
| Votes | Preference Order |
|---|---|
| 12 | B > C > A |
| 11 | A > B > C |
| 5 | C > B> A |
| 4 | A > C > B |
| 4 | C > A > B |
| 0 | B > A > C |
If we look at pairwise elections in this profile, we find that A beats B (19-17), B beats C (23-13), and C beats A (21-15). So in this example there is no Condorcet winner or Condorcet loser. We say that instead there is a Condorcet cycle.
In the interactive mathlet below, explore pairwise elections and the Condorcet winner. Although it seems natural to look at pairwise elections when there are more than two candidates, these elections can often yield no result, forcing us to consider an alternative way to determine a winner.
James E. Hamblin, "Three Party Elections: Interactive Examples - Pairwise Elections and the Condorcet Winner," Convergence (July 2006)




