- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematics Magazine - April 2007
ARTICLES
Minimum Area Venn Diagrams Whose Curves Are Polyominoes
Stirling Chow and Frank Ruskey
Page 95
Three set Venn diagrams are conventionally drawn using three overlapping circles that subdivide the plane into eight regions. Venn diagrams can also be drawn using curves other than circles, and with more than three curves. An n-Venn diagram subdivides the plane into 2n non-empty regions. We consider here the question of whether an n-Venn diagram can be drawn where the subdivision is constrained to consist of 2n - 1 unit squares. In this case the curves must be the outlines of polyominoes, each of area 2n - 1 .
Mom! There's an Astroid in My Closet!
Derek Seiple, Eugene Boman, and Richard Brazier
Page 108
We address the mathematics of closet doors. Specifically we answer the questions, "How much clear floor space is required to open and close a bifold closet door, and what is the boundary curve?" We then generalize the problem to address n-fold doors and show a connection to Archimedes' construction of an ellipse using the Trammel of Archimedes.
Primes and Probability: The Hawkins Random Sieve
John Lorch and Giray Ökten
Page 116
In 1957, David Hawkins developed an elegant probabilistic model for the prime numbers, now known as the Hawkins primes, by randomizing the sieve of Eratosthenes. We survey various applications of the Hawkins primes to well-known results and conjectures in prime distribution theory, and we show that a generalization of the Hawkins primes may be used to model interesting sequences aside from the primes.
NOTES
For All Possible Distances Look to the Permutohedron
Joe Santmyer
Page 120
Every mathematics student is bound to study permutations in a discrete mathematics or abstract algebra course. But will they encounter a permutohedron? What sort of object is a permutohedron? Certainly the name implies that permutations are involved. Take the point (1,2,3,...,n) and all n permutations of its coordinates and you get the vertices of a permutohedron. The permutohedron is an n - 1 dimensional creature living in n dimensional space. Examining the Euclidean distance between the vertices uncovers several interesting and surprising properties regarding their values and their relationship to inversions of a permutation.
Finite Mimicry of Gödel’s Incompleteness Theorem
Fjelstad, Paul
Page 130
This paper seeks to come up with the minimal structure needed to mimic Gödel’s formal system with regard to self-referring sentences, incompleteness, the futility of striving for completeness, and the inability to define the nature of truth. It constructs a set of sentences indexed by a set, and replaces the natural number index set with an arbitrary set that can be finite. In fact it can have as few as two elements.
There is a kind of uncertainty principle at work here. To guarantee consistency, you can go finite, but then you don’t have enough names to code all the sentences in your language. To have enough names, you can go infinite, but you no longer can prove consistency.
Digit Reversal without Apology
Lara Pudwell
Page 133
The number 1089 has the curious property that when one reverses its digits, an integer multiple of itself is obtained. G. H. Hardy observed this fact in his Apology, and claimed that it is not a serious theorem since it cannot be generalized. However, in the 1960s, A. Sutcliffe and T. Kaczynski published results for 2- and 3-digit reversible integers. We extend their work to 4- and 5-digit reversible integers. Specifically, we give a structure theorem for certain sets of reversible integers and show that there exist such integers in every base n ≥ 3.
A Quintile Rule for the Gini Coefficient
Leon Gerber
Page 137
Undergraduate calculus courses for business and economics majors frequently include the Gini coefficient of income inequality, or simply the “Gini coefficient,” as an application of integration. Because the U.S. Census Bureau provides the relevant information in quintiles, Simpson’s rule, which requires an even number of intervals, cannot be used to approximate the integral. Usually the trapezoidal rule is used which, because the Lorenz curve is concave upward, underestimates the Gini coefficient. Here we derive a rule which is exact for fifth-degree polynomials and is just as simple as Simpson’s rule, which is exact only for third-degree polynomials.
A Short Proof of the Two-sidedness of Matrix Inverses
Raymond A. Beauregard
Page 139
We offer a short proof that for any n x n matrices A and C over a field of scalars AC - I if and only if CA =I .
Root Preserving Transformations of Polynomials
Branko Curgus and Vania Mascioni
Page 140
We consider linear transformations on the (real or complex) vector space of polynomials of degree up to a specified integer. We prove (for all non-constant polynomials in the space) that such a transformation has the property that a polynomial and its image always have at least one root in common if and only if the transformation is a multiple of the identity. The proof is elementary and could reasonably find its way into a college classroom.
Do Cyclic Polgyons Make the Cut?
Samuel Otten
Page 142
It is a common misconception (at least among students and laypeople) that mathematical discovery in elementary geometry is complete. However, by mixing together cyclic polygons and cyclic product relations, a new result has been uncovered. The theorem and its proof are easily accessible for the average undergraduate, and generalizations are suggested.
Non Existence of a Composition Law
Saban Alaca and Kenneth S. Williams
Page 146
It is known that every positive odd integer can be expressed in the form x2 + y2 + 2z2 for some integers x, y, and z . Clearly one of x and y must be odd and one must be even. Thus every positive odd integer is of the form
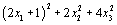
for some integers x1, x2, and x3. Let m and n be positive odd integers. Then mn is also a positive odd integer and there exist integers x1, x2,x3, y1, y2, y3,z1, z2, and z3 such that
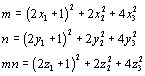
Hence
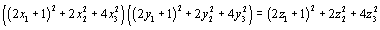
The question naturally arises: Is this equality a consequence of some underlying composition law for the polynomial 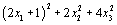 ? We show directly from first principles that it is not.
? We show directly from first principles that it is not.




