- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematics Magazine - December 2007
ARTICLES
Some first tantalizing steps into semigroup theory
Christopher Hollings
Page 331
Semigroup theory is a thriving field in modern abstract algebra, though perhaps not a very well-known one. In this article, we give a brief introduction to the theory of algebraic semigroups and hopefully demonstrate that it has a flavor quite different from that of group theory. In the first few sections, we build up some basic semigroup theory, always with the group analogy at the back of our minds. Then, once we have established enough theory, we break free of this restriction and see some truly ``independent'' semigroup theory. In the final section, we consider the application of semigroups to the study of ``partial symmetries.''
Four Proofs of the Ballot Theorem
Marc Renault
Page 345
Suppose that in an election, candidate A receives a votes and candidate B receives b votes, where a > kb for some positive integer k. How many ways can the a + b ballots be ordered so that A maintains more than k times as many votes as B throughout the counting of the ballots? The solution  , has been known for over a hundred years, and mathematicians have not stopped devising proofs of this result. We present four of the most interesting proofs, describe some of the history surrounding each of the proofs, and consider the different perspectives that each proof brings to the problem.
, has been known for over a hundred years, and mathematicians have not stopped devising proofs of this result. We present four of the most interesting proofs, describe some of the history surrounding each of the proofs, and consider the different perspectives that each proof brings to the problem.
An Intriguing Property of the Center of Mass for Points on Quadratic Curves and Surfaces
Leonid Hanin, Robert Fisher, and Boris Hanin
Page 353
Pick n≥ 2n ¸ 2 arbitrary points  on a circle, denote by C their geometric center of mass, and construct the second points of intersection
on a circle, denote by C their geometric center of mass, and construct the second points of intersection 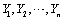 of the respective lines
of the respective lines  with the circle. The article starts with proving the following mind-blowing identity
with the circle. The article starts with proving the following mind-blowing identity

The authors are unaware of the "real" geometrical or physical reason for its validity, nor do they know who first discovered this amazing fact. However, they show that the identity holds true for all quadratic curves and surfaces and, moreover, describe all points C in the plane or 3-dimensional space with the same property.
NOTES
Another Approach to Solving A = mP for Triangles
Tom Leong, Dionne T. Bailey, Elsie M. Campbell, Charles R. Diminnie, and Paul K. Swets.
Page 363
The problem of finding all integer-sided triangles whose area A and perimeter P are numerically equal appears as far back as 1865. Although differing in details, all early solutions required a good deal of trial and error. Not surprisingly, the generalization of solving A = mP for integers m ≥ 2 wasn’t considered until well into the last century. A recent article in this magazine gave an algorithm for completely solving this problem by using Pythagorean Triples. This Note presents another approach which gives a relatively simple characterization of all solutions and essentially relies only on the easy manipulation of a single Diophantine equation.
On the number of Self-Avoiding Walks on Hyperbolic Lattices
Jonathan D. Barry and C. Chris Wu
Page 369
Imagine that you are standing at an intersection in a city where the street system is a square grid. You choose a street at random and begin walking. At each intersection, you choose either to continue straight ahead or to turn left or right. There is only one rule: you must not return to any intersection you have already visited. In other words, your path should be self-avoiding. A fundamental question is: if you walk n blocks, how many possible paths could you have followed?
What we have described above is the self-avoiding walk on the square lattice. Let c(n) be the number of different paths that you can take if you walk n blocks, then it is known that c(n)1/n approaches a positive number b as n approaches infinity. What is the value of b? For the self-avoiding walk on the square lattice, a trivial bound for b is between 2 and 3. We will study b for self-avoiding walks on hyperbolic lattice H(v,p) (defined in the paper) and give a good bound for b. For example, we show that b lies between 3.90525 and 4 on .
Uncountable Sets and an Infinite Real Number Game
Matthew Baker
Page 377
We give a short proof of the well-known fact that the unit interval [0,1] is uncountable by means of a simple infinite game. We also show using this game that a (non-empty) perfect subset of [0,1] must be uncountable.
When Multiplication Mixes Up Digits
David Wolfe
Page 380
Many multiples of the number 123456789 are pandigital, meaning that they permute all 9 digits. For example, 123456789 times 4 is 493827156. We generalize this observation to any base, proving that the product is pandigital whenever the single digit multiplier (4) is relatively prime to the base minus one (9).
No Fooling! Newton’s Method Can Be Fooled
Peter Horton
Page 383
The success and rapid convergence of Newton’s method tends to make people think that it is infallible. Various examples of convergent Newton sequences which do not converge to a zero of the underlying function are given.
On Antiderivaties of the Zero Function
Michael Range
Page 387
We discuss an intuitive direct proof of the fact that functions with zero derivative must be constant, which turns into a rigorous proof by simply invoking the completeness of the real numbers.
MATH BITE
Six Famous Mathematicians
Ronald E. Prather
Page 390
A crossword puzzle in which, once solved, the names of six famous mathematicians are embedded.
PROOF WITHOUT WORDS
An Algebraic Inequality
Jaing, Wei-Dong
Page 344
We solve an algebraic inequality that has appeared in different forms on the Leningrad Mathematics Olympiad and on the Australian Mathematics Olympiad by arranging subsquares of varying sizes inside a square.




