- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematics Magazine - February 2008
ARTICLES
On Infinitely Nested Radicals
Seth Zimmerman and Chungwu Ho
pp. 3-15
Most of us were shown that 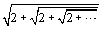 equals 2 long before we were troubled by convergence, or even knew what it meant. We might have taken special delight in seeing the golden mean emerge from the snake-like
equals 2 long before we were troubled by convergence, or even knew what it meant. We might have taken special delight in seeing the golden mean emerge from the snake-like  . This paper investigates such infinitely nested radicals, considering general forms like
. This paper investigates such infinitely nested radicals, considering general forms like  , where a and b are rational. Under what conditions do these converge? Can any given real number be a limit? What patterns do families of these radicals create on the number line? All of these questions are considered here, most of them resolved by proof.
, where a and b are rational. Under what conditions do these converge? Can any given real number be a limit? What patterns do families of these radicals create on the number line? All of these questions are considered here, most of them resolved by proof.
Synthetic Partial Fraction Decompositions
William A. Adkins and Mark Davidson
pp. 16-26
The partial fraction decomposition of a general rational function over the real numbers has been routinely treated in calculus texts, where the procedure is normally taught, via the technique of undetermined coefficients. As has been observed numerous times, there is an alternative algorithmic method for partial fraction decompositions that primarily involves repeated division by polynomials. The goal of this article is to present the partial fraction decomposition algorithm in a format that is amenable to recursive hand calculations in calculus or differential equations classes. These are calculations that are done on the coefficients of the polynomials involved, and hence we refer to the method as synthetic partial fraction decomposition, due to the use of synthetic division by linear and quadratic polynomials. A Brief History of Impossibility
Jeff Suzuki
pp. 27-38
Polynomial Root Squeezing
Matthew Boelkins, Justin From, and Samuel Kolins
pp.39-44
Given a real polynomial with distinct real zeros, the Polynomial Root Dragging Theorem states that if one or more zeros of the polynomial are moved to the right, then all of the critical numbers also move to the right with none of the critical numbers moving as much as the root that is moved most. But what happens if some of the roots of the polynomial are dragged in opposing directions, either toward or away from each other? The Polynomial Root Squeezing Theorem shows that when two zeros of a polynomial are squeezed together, the outermost critical numbers move inward. We then apply the Root Squeezing Theorem to prove results about which polynomials have derivatives with minimum span; that is, the distance from their derivatives’ smallest to greatest zeros is the least possible.
NOTES
Paint it Black - A Combinatorial Yawp
Arthur T. Benjamin, Jennifer J. Quinn, James A. Sellers, and Mark A. Shattuck
pp. 45-50
We begin by solving a problem posed from the Monthly. Show
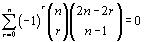
. We prove this combinatorially by pairing up objects that have an odd value of r with objects that have an even value of r. The proof, and its generalizations, lead to many new and interesting identities.
Integration by Parts and Infinite Series
Shelby J. Kilmer
pp. 51-54
Sometimes tabular integration by parts doesn’t terminate, and when this happens, an infinite series is formed. Using this method we derive infinite series for the sine, cosine, and exponential functions and several for pi. We also give criteria for the convergence of such a series.
What Fraction of a Soccer Ball is Covered with Pentagons?
P.K. Aravind
pp. 55-57
Many soccer balls have their surface covered with a pattern consisting of twelve pentagons and twenty hexagons. We use elementary geometric methods to calculate the fraction of the area of the soccer ball covered by the pentagons.
Euler’s Triangle Inequality via Proofs Without Words
Roger B. Nelsen
pp. 58-61
Euler’s triangle inquality states that  , where R and r denote, respectively, the circumradius and the inradius of a triangle. In this Note we use “proofs without words ” to prove three simple lemmas that can be combined with the arithmetic mean – geometric mean inequality to reduce the proof of Euler’s triangle inequality to simple algebra.
, where R and r denote, respectively, the circumradius and the inradius of a triangle. In this Note we use “proofs without words ” to prove three simple lemmas that can be combined with the arithmetic mean – geometric mean inequality to reduce the proof of Euler’s triangle inequality to simple algebra.
PROOF WITHOUT WORDS
Double Angle Formula via Area
James D. Currie
pp.62
A triangle labeled two different ways verifies the double angle formula for sines.
The Cauchy–Schwarz Inequality
Sidney Kung
A rectangular area is partitioned two different ways to demonstrate the Cauchy–Schwarz Inequality for vectors in two dimensions.
PROBLEMS
pp. 63-69
REVIEWS
pp. 70
REVIEW
67th Annual William Lowell Putnam Exam Solutions
pp. 72




